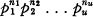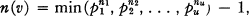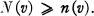Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bose, R. C.
and
Shrikhande, S. S.
1960.
On the Composition of Balanced Incomplete Block Designs.
Canadian Journal of Mathematics,
Vol. 12,
Issue. ,
p.
177.
Bose, R. C.
Chakravarti, I. M.
and
Knuth, D. E.
1960.
On Methods of Constructing Sets of Mutually Orthogonal Latin Squares Using a Computer. I.
Technometrics,
Vol. 2,
Issue. 4,
p.
507.
Taussky, Olga
1960.
Matrices of rational integers.
Bulletin of the American Mathematical Society,
Vol. 66,
Issue. 5,
p.
327.
Ostrowski, R. T.
and
Van Duren, K. D.
1961.
On a theorem of Mann on Latin squares.
Mathematics of Computation,
Vol. 15,
Issue. 75,
p.
293.
Bose, R. C.
Chakravarti, I. M.
and
Knuth, D. E.
1961.
On Methods of Constructing Sets of Mutually Orthogonal Latin Squares Using a Computer. II.
Technometrics,
Vol. 3,
Issue. 1,
p.
111.
Parker, E. T.
1962.
Nonextendibility conditions on mutually orthogonal Latin squares.
Proceedings of the American Mathematical Society,
Vol. 13,
Issue. 2,
p.
219.
Weisner, Louis
1963.
Special Orthogonal Latin Squares of Order 10.
Canadian Mathematical Bulletin,
Vol. 6,
Issue. 1,
p.
61.
Golomb, S.
and
Posner, E.
1964.
Rook domains, Latin squares, affine planes, and error-distributing codes.
IEEE Transactions on Information Theory,
Vol. 10,
Issue. 3,
p.
196.
YATES, F.
1965.
Contributions to Statistics.
p.
485.
Clatworthy, Willard H.
1967.
Some New Families of Partially Balanced Designs of the Latin Square Type and Related Designs.
Technometrics,
Vol. 9,
Issue. 2,
p.
229.
Hanani, Haim
1968.
DIVISION OF MATHEMATICS: SOME COMBINATORIAL CONFIGURATIONS*.
Transactions of the New York Academy of Sciences,
Vol. 30,
Issue. 3 Series II,
p.
421.
Jaech, J. L.
1969.
The Latin Square.
Journal of Quality Technology,
Vol. 1,
Issue. 4,
p.
242.
Hanani, Haim
1970.
On the number of orthogonal latin squares.
Journal of Combinatorial Theory,
Vol. 8,
Issue. 3,
p.
247.
Bush, K.A
1971.
Unbalanced Hadamard matrices and finite projective planes of even order.
Journal of Combinatorial Theory, Series A,
Vol. 11,
Issue. 1,
p.
38.
1971.
Principles of Combinatorics.
Vol. 72,
Issue. ,
p.
1.
Lawless, J.F
1971.
Note on a family of BIBD's and sets of mutually orthogonal Latin squares.
Journal of Combinatorial Theory, Series A,
Vol. 11,
Issue. 1,
p.
101.
Bush, K. A.
1971.
An inner orthogonality of Hadamard matrices.
Journal of the Australian Mathematical Society,
Vol. 12,
Issue. 2,
p.
242.
Hedayat, A.
1971.
A Set of Three Mutually Orthogonal Latin Squares of Order 15.
Technometrics,
Vol. 13,
Issue. 3,
p.
696.
1971.
Elements of Combinatorial Computing.
p.
243.
Wilson, Richard M
1972.
An existence theory for pairwise balanced designs I. Composition theorems and morphisms.
Journal of Combinatorial Theory, Series A,
Vol. 13,
Issue. 2,
p.
220.