Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rider, Daniel
1966.
A relation between a theorem of Bohr and Sidon sets.
Bulletin of the American Mathematical Society,
Vol. 72,
Issue. 3,
p.
558.
Chaney, R. W.
1969.
On uniformly approximable Sidon sets.
Proceedings of the American Mathematical Society,
Vol. 21,
Issue. 1,
p.
245.
Parker, Willard A.
1972.
Central Sidon and central ∧p sets.
Journal of the Australian Mathematical Society,
Vol. 14,
Issue. 1,
p.
62.
McGehee, O. Carruth
1972.
Conference on Harmonic Analysis.
Vol. 266,
Issue. ,
p.
229.
Edwards, Robert E.
Hewitt, Edwin
and
Ross, Kenneth A.
1972.
Conference on Harmonic Analysis.
Vol. 266,
Issue. ,
p.
35.
Ragozin, David L
1974.
Zonal measure algebras on isotropy irreducible homogeneous spaces.
Journal of Functional Analysis,
Vol. 17,
Issue. 4,
p.
355.
Dudley, E.
1975.
The Gaussian law and the law of the iterated logarithm for lacunary sets of characters.
Transactions of the American Mathematical Society,
Vol. 214,
Issue. 0,
p.
187.
Drury, S. W.
1975.
Birelations and Sidon sets.
Proceedings of the American Mathematical Society,
Vol. 53,
Issue. 1,
p.
123.
Hutchinson, M. F.
1977.
Non-tall compact groups admit infinite Sidon sets.
Journal of the Australian Mathematical Society,
Vol. 23,
Issue. 4,
p.
467.
Graham, Colin C.
1977.
Functional calculus and positive-definite functions.
Transactions of the American Mathematical Society,
Vol. 231,
Issue. 1,
p.
215.
Dudley, E.
and
Hall, P.
1979.
The Gaussian law and lacunary sets of characters.
Journal of the Australian Mathematical Society,
Vol. 27,
Issue. 1,
p.
91.
Vrem, Richard C.
1991.
Independent sets and lacunarity for hypergroups.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 50,
Issue. 2,
p.
171.
Li, D.
Queffélec, H.
and
Rodríguez-Piazza, L.
2002.
Some new thin sets of integers in harmonic analysis.
Journal d'Analyse Mathématique,
Vol. 86,
Issue. 1,
p.
105.
Ramsey, Thomas
and
Graham, Colin
2006.
Planar Sidonicity and quasi-independence for multiplicative subgroups of the roots of unity.
Pacific Journal of Mathematics,
Vol. 225,
Issue. 2,
p.
325.
Sanders, T.
2007.
The Littlewood-Gowers problem.
Journal d'Analyse Mathématique,
Vol. 101,
Issue. 1,
p.
123.
Graham, Colin C.
and
Hare, Kathryn E.
2013.
Interpolation and Sidon Sets for Compact Groups.
p.
1.
Graham, Colin C.
and
Hare, Kathryn E.
2013.
Interpolation and Sidon Sets for Compact Groups.
p.
49.
Graham, Colin C.
and
Hare, Kathryn E.
2013.
Interpolation and Sidon Sets for Compact Groups.
p.
77.
Graham, Colin C.
and
Hare, Kathryn E.
2013.
Interpolation and Sidon Sets for Compact Groups.
p.
117.
Graham, Colin C.
and
Hare, Kathryn E.
2013.
Interpolation and Sidon Sets for Compact Groups.
p.
175.

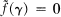 for all
for all