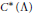Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pask, David
Rennie, Adam
and
Sims, Aidan
2008.
The noncommutative geometry of k-graph C*-algebras.
Journal of K-Theory,
Vol. 1,
Issue. 2,
p.
259.
Allen, Stephen
2008.
A Gauge Invariant Uniqueness Theorem for Corners of Higher Rank Graph Algebras.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 6,
Davidson, Kenneth R.
Power, Stephen C.
and
Yang, Dilian
2008.
Atomic representations of rank 2 graph algebras.
Journal of Functional Analysis,
Vol. 255,
Issue. 4,
p.
819.
PASK, DAVID
RAEBURN, IAIN
and
WEAVER, NATASHA A.
2009.
A family of 2-graphs arising from two-dimensional subshifts.
Ergodic Theory and Dynamical Systems,
Vol. 29,
Issue. 5,
p.
1613.
LEWIN, PETER
and
SIMS, AIDAN
2010.
Aperiodicity and cofinality for finitely aligned higher-rank graphs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 149,
Issue. 2,
p.
333.
Evans, D. Gwion
and
Sims, Aidan
2012.
When is the Cuntz–Krieger algebra of a higher-rank graph approximately finite-dimensional?.
Journal of Functional Analysis,
Vol. 263,
Issue. 1,
p.
183.
Kumjian, Alex
Pask, David
and
Sims, Aidan
2013.
On theK-theory of twisted higher-rank-graphC∗-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 401,
Issue. 1,
p.
104.
Brownlowe, Nathan
and
Raeburn, Iain
2013.
Two families of Exel–Larsen crossed products.
Journal of Mathematical Analysis and Applications,
Vol. 398,
Issue. 1,
p.
68.
Brown, Jonathan H.
Nagy, Gabriel
and
Reznikoff, Sarah
2014.
A generalized Cuntz–Krieger uniqueness theorem for higher-rank graphs.
Journal of Functional Analysis,
Vol. 266,
Issue. 4,
p.
2590.
Maloney, Ben
Pask, David
and
Raeburn, Iain
2014.
Skew-products of higher-rank graphs and crossed products by semigroups.
Semigroup Forum,
Vol. 88,
Issue. 1,
p.
162.
Kang, Sooran
and
Pask, David
2014.
Aperiodicity and primitive ideals of row-finite k-graphs.
International Journal of Mathematics,
Vol. 25,
Issue. 03,
p.
1450022.
BROWN, JONATHAN
CLARK, LISA ORLOFF
and
SIERAKOWSKI, ADAM
2015.
Purely infinite -algebras associated to étale groupoids.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 8,
p.
2397.
Brown, Jonathan H.
and
an Huef, Astrid
2015.
The Socle and Semisimplicity of a Kumjian–Pask Algebra.
Communications in Algebra,
Vol. 43,
Issue. 7,
p.
2703.
Clark, Lisa Orloff
an Huef, Astrid
and
Sims, Aidan
2016.
AF-embeddability of 2-graph algebras and quasidiagonality of k-graph algebras.
Journal of Functional Analysis,
Vol. 271,
Issue. 4,
p.
958.
Kumjian, Alex
Pask, David
Sims, Aidan
and
Whittaker, Michael F.
2016.
Topological spaces associated to higher-rank graphs.
Journal of Combinatorial Theory, Series A,
Vol. 143,
Issue. ,
p.
19.
Clark, Lisa Orloff
and
Pangalela, Yosafat E.P.
2017.
Kumjian–Pask algebras of finitely aligned higher-rank graphs.
Journal of Algebra,
Vol. 482,
Issue. ,
p.
364.
Farsi, Carla
Gillaspy, Elizabeth
Kang, Sooran
and
Packer, Judith
2017.
Excursions in Harmonic Analysis, Volume 5.
p.
35.
an Huef, Astrid
Kang, Sooran
and
Raeburn, Iain
2017.
KMS States on the Operator Algebras of Reducible Higher-Rank Graphs.
Integral Equations and Operator Theory,
Vol. 88,
Issue. 1,
p.
91.
Larki, Hossein
2018.
Purely infinite simple Kumjian–Pask algebras.
Forum Mathematicum,
Vol. 30,
Issue. 1,
p.
253.
Ara, Pere
Hazrat, Roozbeh
Li, Huanhuan
and
Sims, Aidan
2018.
Graded Steinberg algebras and their representations.
Algebra & Number Theory,
Vol. 12,
Issue. 1,
p.
131.