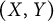General Toeplitz kernels and $(X,Y)$-invariance

Abstract

Motivated by the near invariance of model spaces for the backward shift, we introduce a general notion of $(X,Y)$-invariant operators. The relations between this class of operators and the near invariance properties of their kernels are studied. Those lead to orthogonal decompositions for the kernels, which generalize well-known orthogonal decompositions of model spaces. Necessary and sufficient conditions for those kernels to be nearly X-invariant are established. This general approach can be applied to a wide class of operators defined as compressions of multiplication operators, in particular to Toeplitz operators and truncated Toeplitz operators, to study the invariance properties of their kernels (general Toeplitz kernels).

1 Introduction

Invariant subspaces play an important role in the study of operators. In particular, shift invariant subspaces (with various definitions) have attracted much attention in mathematics and engineering. For instance, Beurling’s theorem characterizes all nontrivial shift invariant subspaces of the Hardy space $H^2:=H^2(\mathbb {D})$ ( $\mathbb {D}$ is the unit disk), where the shift operator is multiplication by z, as being of the form $\theta H^2$ , where $\theta $ is an inner function. From this result, one can deduce that all nontrivial $S^*$ -invariant subspaces of $H^2$ are of the form ${K^2_{\theta }}=H^2\ominus \theta H^2$ ; these are called model spaces. They provide the natural setting for truncated Toeplitz operators (see (2.8)), which have generated enormous interest and are important in connection with applications in mathematics, physics, and engineering (see, for instance, [15]).

Model spaces can also be seen as a particular case of Toeplitz kernels, i.e., kernels of Toeplitz operators with symbol $\bar \theta $ (for definition of Toeplitz operator, see (2.5)). Kernels of Toeplitz operators are not, in general, $S^*$ -invariant subspaces of $H^2$ , but they are nearly $S^*$ -invariant. We say that a closed subspace $M \subset H^2$ is nearly $S^*$ -invariant if

(1.1) $$ \begin{align} \text{ for all } f\in M \text{ such that } f(0)=0, \text{ we have } S^*f\in M. \end{align} $$

Nearly $S^*$ -invariant subspaces were first introduced by Hitt [20], following Hayashi’s work on kernels of Toeplitz operators [19]. These results were resumed and further developed by Sarason in [28, 29] and since then nearly $S^*$ -invariant subspaces have been studied by many mathematicians. Hitt proved, in particular, the following.

Theorem 1.1 [20]

Any nontrivial nearly $S^*$ -invariant subspace of $H^2$ has the form ${N=g K}$ , where g is the element of N of unit norm which has a positive value at the origin and is orthogonal to all elements in N vanishing at $0$ , K is an $S^*$ -invariant subspace and the operator $M_g$ is an isometry from K into $H^2$ .

Hayashi gave a complete characterization of the nearly $S^*$ -invariant subspaces which are kernels of Toeplitz operators as being those where g is outer and $g^2$ is a rigid function.

Recently, nearly $S^*$ -invariant subspaces of $H^2$ with finite defect $m\in \mathbb {N}$ were introduced in [11] and their study has quickly attracted attention [12, 22, 27]. In most of these papers, the emphasis is put on characterizations of those spaces in terms of model spaces which generalize Hitt’s results.

Here, we will not take the same approach; rather we will study conditions for the kernels of operators in a wide class to be nearly invariant, or almost invariant (see Definition 1.4), in connection with certain invariance properties of the operators and with orthogonal decompositions of their kernels generalizing well-known orthogonal decomposition of the model spaces.

We also adopt a more general setting, by studying invariance properties with respect to a general operator $X\in \mathcal {B}(\mathcal {H})$ . This is motivated by the following observation. Imposing a zero at $0$ for f in (1.1) is equivalent to imposing that $\bar z f\in H^2$ , in which case $S^*f=\bar z f$ . So (1.1) can be equivalently reformulated as

(1.2) $$ \begin{align} \text{if } f\in M, \; \bar zf\in H^2, \text{ then } \bar z f\in M, \end{align} $$

which is the reason why nearly $S^*$ -invariant spaces are also called nearly $M_{\bar z}$ -invariant, or simply nearly $\bar z$ -invariant (in $H^2$ ) [7]. More generally, for any function $\eta $ in a wide class, including all $\eta \in \overline {H^{\infty }}$ [7], Toeplitz kernels are nearly $\eta $ -invariant, meaning that for a Toeplitz kernel $\ker T$ ,

(1.3) $$ \begin{align} \text{if } f\in \ker T, \; \eta f\in H^2, \text{ then } \eta f\in \ker T. \end{align} $$

Definition 1.2 Let $\mathcal {H}$ , H be Hilbert spaces such that $H\subset \mathcal {H}$ . Let $\mathcal {L}\neq \{0\}$ be a closed subspace of H, and let $X\in \mathcal {B}(\mathcal {H})$ . We say that $\mathcal {L}$ is nearly X-invariant w.r.t. (with respect to) H if and only if, for all $h\in \mathcal {L}$ , such that $Xh\in H$ we have $Xh\in \mathcal {L}$ . If there exists a finite dimensional space $\mathcal {F}\subset H$ such that, for all $h\in \mathcal {L}$ with $Xh\in H$ , we have ${Xf\in \mathcal {L}\oplus \mathcal {F}}$ , we say that $\mathcal {L}$ is nearly X-invariant w.r.t. H with defect m, where m is the smallest dimension of such subspace $\mathcal {F}$ .

Two other related definitions are the following.

Definition 1.3 Let $\mathcal {L}\neq \{0\}$ be a closed subspace of $H \subset \mathcal {H}$ , and let $X\in \mathcal {B}(\mathcal {H})$ . We say that $\mathcal {L}$ is H-stable for X if $X\mathcal {L}\subset H$ .

Definition 1.4 A subspace $\mathcal {L} \subset \mathcal {H}$ is said to be almost-invariant for the operator ${X\in \mathcal {B}(\mathcal {H})}$ if there exists a finite dimensional space $\mathcal {F} \subset \mathcal {H}$ such that

$$ \begin{align*} X\mathcal{L} \subset \mathcal{L}\oplus \mathcal{F}. \end{align*} $$

The smallest possible dimension of $\mathcal {F}$ is called the defect of $\mathcal {L}$ .

Remark 1.5 As above let $\mathcal {L}\subset H\subset \mathcal {H}$ , and let $X\in \mathcal {B}(\mathcal {H})$ . It is clear that if $\mathcal {L}$ is nearly X-invariant w.r.t. H with defect m and $\mathcal {L}$ is H-stable for X, then $\mathcal {L}$ is almost-invariant for X with defect m.

Near X-invariance can be interpreted as meaning that, under the action of X, any element of $\mathcal {L}$ is mapped either into $\mathcal {L}$ or into $\mathcal {H}\setminus H$ ; no element of $\mathcal {L}$ is mapped into $H \setminus \mathcal {L}$ . We can interpret X-invariance with defect analogously. On the other hand, this can be related, for model spaces, with certain orthogonal decompositions. For example, if $\alpha $ and $\theta $ are inner functions with $\alpha < \theta $ (i.e., $\tfrac {\theta }\alpha \in H^{\infty }$ and $\tfrac {\theta }\alpha \notin \mathbb {C}$ ), then we have two well-known decompositions:

1. (i) ${K^2_{\theta }}=\alpha K^2_{\frac {\theta }{\alpha }}\oplus {K^2_{\alpha }}\quad \quad $ and

2. (ii) ${K^2_{\theta }}=K^2_{\frac {\theta }{\alpha }}\oplus \frac {\theta }{\alpha }{K^2_{\alpha }}$ .

In the case (i), the first term in the orthogonal sum is such that $\bar \alpha (\alpha K^2_{\frac {\theta }{\alpha }})\subset {K^2_{\theta }}$ , whereas for the second term, we have $\bar \alpha {K^2_{\alpha }}\subset H^2_-:=\bar z \overline {H^2}$ . So the multiplication operator $M_{\bar \alpha }$ maps any element of ${K^2_{\theta }}$ either into ${K^2_{\theta }}$ or into $L^2\setminus H^2$ . Thus the orthogonal decomposition (i) reflects the fact that ${K^2_{\theta }}$ is nearly $\bar \alpha $ -invariant w.r.t. $H^2$ .

In the case (ii), we see that the first term is mapped by the multiplication operator $M_{\alpha }$ into ${K^2_{\theta }}$ , whereas the second term is mapped into $H^2\setminus {K^2_{\theta }}$ . So the decomposition (ii) can be seen as reflecting the fact that ${K^2_{\theta }}$ is $H^2$ -stable for $M_{\alpha }$ and, if $\dim {K^2_{\alpha }} <\infty $ , it is almost-invariant for $M_{\alpha }|_{H^2}$ , i.e., the Toeplitz operator $T_{\alpha }$ .

Since model spaces are particular cases of Toeplitz kernels, a natural question arises: is it possible to obtain, for more general kernels of operators, orthogonal decompositions that generalize those that are known for model spaces and allow us to establish conditions for their being nearly invariant or almost-invariant with respect to a given operator?

The near $S^*$ -invariance of Toeplitz kernels can also be related with the fact that Toeplitz operators T are shift-invariant [2], i.e., for any $f,g\in H^2$ , we have

(1.4) $$ \begin{align} \langle Tf,g\rangle = \langle Tzf,zg\rangle. \end{align} $$

Indeed, if $f\in \ker T$ and $\bar z f\in H^2$ , then from (1.4), we have $\langle T\bar zf,g\rangle = \langle Tf,zg\rangle =0$ for any $g\in H^2$ , since $Tf=0$ ; therefore, $\bar z f\in \ker T$ . We see, thus, that the near $S^*$ -invariance of Toeplitz kernels can be derived from the shift-invariance of Toeplitz operators. A second natural question arises from this observation: how are certain invariance properties of an operator related with those of its kernel?

In this paper, we study these questions. We extend the notion of shift-invariant operator (thus including, in particular, the usual notion of shift-invariant operator in applications [32]), and we generalize the concept of nearly $S^*$ -invariant subspace, possibly with defect.

In Section 2, we study some basic properties of $(X,Y)$ -invariant operators and we focus on compressions of multiplication operators to closed subspaces of $L^2$ , showing in particular that those compressions are X-invariant for all $X\in L^{\infty }$ (so, in particular, they are all shift-invariant). In Section 3, we study the relations between X-invariance of operators and the near invariance properties of their kernels, and in Section 4, we show that those relations lead to orthogonal decompositions for the kernels, which generalize well-known orthogonal decompositions of model spaces. These results allow us to establish necessary and sufficient conditions for those kernels to be nearly X-invariant, with or without defect. They also allow for a general approach to the study of a wide class of operators defined as compressions of multiplications operators (general Toeplitz operators [6]) and the invariance properties of their kernels (general Toeplitz kernels). In Sections 5 and 6, we apply those results to Toeplitz operators and truncated Toeplitz operators.

2 $(X, Y)$ -invariant operators

Let $\mathcal {H}$ , $\mathcal {K}$ be Hilbert spaces. Let X be a bounded linear operator on $\mathcal {H}$ , i.e., $X\in \mathcal {B}(\mathcal {H})$ . Let $Y\in \mathcal {B}(\mathcal {K})$ , and let $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ be closed subspaces. We will use the notation

(2.1) $$ \begin{align} H_X=\{f\in H: Xf\in H\}\quad \text { and } \quad K_Y=\{g\in K : Yg\in K\}. \end{align} $$

An operator $A\in \mathcal {B}(H,K)$ is called $(X,Y)$ -invariant if and only if we have

(2.2) $$ \begin{align} \langle AXf,g\rangle=\langle Af,Yg \rangle \quad \text{for all }\quad f\in H_X, g\in K_Y. \end{align} $$

In particular, if $X\in \mathcal {B}(\mathcal {H})$ and $A\in \mathcal {B}(H)$ , we say that A is X-invariant if and only if

(2.3) $$ \begin{align} \langle AXf,g\rangle=\langle Af,X^*g \rangle \quad \mathrm{for}\quad f\in H_X, g\in H_{X^*}, \end{align} $$

i.e., A is $(X,X^*)$ -invariant.

Proposition 2.1 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Then:

1. (1) If $AX=Y^*A$ on $H_X$ , then A is $(X,Y)$ -invariant.

2. (2) A is $(X,Y)$ -invariant if and only if $A^*$ is $(Y,X)$ -invariant.

3. (3) If $A\in \mathcal {B}(H)$ and $AX=XA$ on $H_X$ , then A is X-invariant.

Now let $P_{H_X}$ denote the orthogonal projection

$$ \begin{align*} P_{H_X}\colon \mathcal{H} \to H_X. \end{align*} $$

We will also denote by $P_{H_X}$ , whenever the context is clear, the orthogonal projection from H onto $H_X$ .

Note that if X is a co-isometry, i.e., $XX^*=I$ , then

(2.4) $$ \begin{align} f\in H_{X^*} \ \text{ if and only if }\ X^*f\in H_X. \end{align} $$

Lemma 2.2 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Then the following are equivalent:

1. (1) $\langle AXf,Y^*g_1\rangle =\langle Af,g_1 \rangle $ for $f\in H_X$ and $g_1\in K_{Y^*}$ ;

2. (2) $ P_{K_{Y^*}}A|_{H_X} = P_{K_{Y^*}} (YAX)|_{H_X}$ .

Proof Note that, for all $f\in H_X$ and $g_1\in K_{Y^*}$ , we have

$$ \begin{align*}\langle AXf,Y^*g_1\rangle=\langle YAXf,g_1 \rangle=\langle P_{K_{Y^*}}(YAXf), g_1\rangle\end{align*} $$

and

$$ \begin{align*}\langle Af,g_1 \rangle =\langle P_{K_{Y^*}}(Af), g_1\rangle.\end{align*} $$

Thus, the lemma holds.

Lemma 2.3 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Assume that Y is a co-isometry. If A is $(X,Y)$ -invariant, then $P_{K_{Y^*}}A|_{H_X} = P_{K_{Y^*}} (YAX)|_{H_X}$ .

Proof Let $f\in H_X$ and $g_1=YY^*g_1\in K_{Y^*}$ . Then, by (2.4), $g=Y^*g_1\in K_Y$ . Since A is $(X,Y)$ -invariant, then

$$ \begin{align*}\langle AXf,Y^*g_1 \rangle =\langle Af, YY^* g_1\rangle=\langle Af, g_1\rangle.\end{align*} $$

Now the result follows from Lemma 2.2.

Proposition 2.4 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Assume that X and Y are co-isometries. If A is $(X,Y)$ -invariant, then A is $(X^*,Y^*)$ -invariant.

Proof For all $f_1\in H_{X^*}$ , $g_1\in K_{Y^*}$ , we have that $X^*f_1\in H_X$ , $Y^*g_1\in K_Y$ , and

$$ \begin{align*}\langle AX^* f_1,g_1\rangle=\langle AX^*f_1, YY^*g_1\rangle=\langle AXX^*f_1,Y^*g_1\rangle=\langle Af_1,Y^*g_1\rangle.\\[-32pt]\end{align*} $$

Proposition 2.5 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . If Y is unitary, then the following are equivalent:

1. (1) A is $(X,Y)$ -invariant.

2. (2) $\langle AXf,Y^*g_1\rangle =\langle Af,g_1 \rangle $ for $f\in H_X$ and $g_1\in K_{Y^*}$ .

3. (3) $ P_{K_{Y^*}}A|_{H_X} = P_{K_{Y^*}} (YAX)|_{H_X}$ .

If moreover X is unitary, then the above are equivalent to

1. (4) A is $(X^*,Y^*)$ -invariant.

Denote

$$\begin{align*}\mathcal{S}(X,Y)=\{A\in \mathcal{B}(H,K)\colon A \text{ is } (X,Y)\text{-invariant}\}.\end{align*}$$

Clearly, $\mathcal {S}(X,Y)$ is a subspace of $\mathcal {B}(H,K)$ .

Proposition 2.6 Let $H=\mathcal {H}=K=\mathcal {K}$ and $X\in \mathcal {B}(H)$ . Then $\mathcal {S}(X,X^*)=\{X\}'=\{T\in \mathcal {B}(H): TX=XT\}$ .

Let $\varphi \in L^{\infty }$ . The linear operator $T_{\varphi }\in \mathcal {B}(H^2)$ is called a Toeplitz operator with the symbol $\varphi $ if

(2.5) $$ \begin{align}T_{\varphi} f=P_{H^2}(\varphi f)\qquad\text{ for}\quad f\in H^2. \end{align} $$

The Toeplitz operator $T_z$ is usually denoted by S and identified with the unilateral shift. Due to the Brown–Halmos characterization of Toeplitz operators, that is, $A\in \mathcal {B}(H^2)$ is a Toeplitz operator if and only if $S^*AS=A$ , we have the following.

Example 2.7 Let $\mathcal {H}=H=H^2=\mathcal {K}=K$ , $X=S=T_z$ , $Y=S^*$ . Then $H_X=K_{Y^*}=H^2$ and (3) in Proposition 2.5 is just Brown–Halmos condition, $S^*AS=A$ . Therefore, $A\in \mathcal {B}(H^2)$ is a Toeplitz operator if and only if it is S-invariant, ( $(S,S^*)$ -invariant).

Note also that taking $\mathcal {H}=\mathcal {K}=L^2$ , $X=M_z$ , $Y=M_{\bar z}$ and $H=K=H^2$ , $H_X=K_{Y^*}=H^2$ , then (3) in Proposition 2.5 gives

$$\begin{align*}A=P_{H^2}A_{|_{H^2}}=P_{H^2}M_{\bar z}A{M_z}_{|_{H^2}}=S^*AS.\end{align*}$$

So we also can say that $A\in \mathcal {B}(H^2)$ is a Toeplitz operator if and only if it is $M_z$ -invariant,( $(M_z,M_{\bar z})$ -invariant).

It is also worth noting that, by Proposition 2.5, each Toeplitz operator $A=T_{\varphi }$ , $\varphi \in L^{\infty }$ , is $(M_{\bar z},M_{z})$ -invariant. Indeed, for all $f\in (H^2)_{M_{\bar z}}$ , $g\in (H^2)_{M_z}$ , we have

(2.6) $$ \begin{align} \langle T_{\varphi} M_{\bar z}f, g \rangle=\langle \varphi \bar z f, g\rangle=\int_{\mathbb{T}}\varphi \bar z f\bar g dm=\langle \varphi f, zg\rangle =\langle T_{\varphi} f, M_z g\rangle. \end{align} $$

Recall the definition of Hankel operators. Let $J\in \mathcal {B}( L^2)$ , $(Jf)(z)=\bar z f(\bar z)$ . Denote by $\Gamma _{\psi }$ the Hankel operator with symbol $\psi \in L^{\infty }$ defined as $\Gamma _{\psi } \colon H^2\to H^2$ , $\Gamma _{\psi } f=P_{H^2}J\psi f$ for $f\in H^2$ . It is known that an operator $\Gamma \in \mathcal {B}(H^2)$ is a Hankel operator if and only if

(2.7) $$ \begin{align} S^*\Gamma=\Gamma S. \end{align} $$

Hence, we have the following.

Example 2.8 Let $\mathcal {H}=H=H^2=\mathcal {K}=K$ . Then $A\in \mathcal {B}(H^2)$ is a Hankel operator if and only if it is $(S,S)$ -invariant.

Let $\alpha ,\theta $ be nonconstant inner functions. Consider the model spaces $K^2_{\alpha }=H^2\ominus \alpha H^2$ and $K^2_{\theta }=H^2\ominus \theta H^2$ , and let $P_{\alpha }$ , $P_{\theta }$ denote the orthogonal projections from $L^2$ onto $K^2_{\alpha }$ and $ K^2_{\theta }$ , respectively. It is known that $K^2_{\alpha } \cap L^{\infty }$ is dense in $K^2_{\alpha }$ . Let $\varphi \in L^2$ . Define

(2.8) $$ \begin{align}A^{\alpha,\theta}_{\varphi} f=P_{\theta}(\varphi f)\qquad\text{ for}\quad f\in K^2_{\alpha}\cap L^{\infty}.\end{align} $$

If $A^{\alpha ,\theta }_{\varphi }$ can be extended to a bounded operator from $K^2_{\alpha }$ to $K^2_{\theta }$ , i.e., $A^{\alpha ,\theta }_{\varphi }\in \mathcal {B}(K^2_{\alpha },K^2_{\theta })$ , then it is called the asymmetric truncated Toeplitz operator [3]. In particular, if $\theta =\alpha $ , it is called a truncated Toeplitz operator and the notation $A^{\alpha }_{\varphi } =A^{\alpha ,\alpha }_{\varphi }$ will be used. In [30], Sarason showed that an operator $A\in \mathcal {B} (K^2_{\theta })$ is a truncated Toeplitz operator if and only if

(2.9) $$ \begin{align}\langle Azf,zg\rangle=\langle Af,g \rangle\quad\text{for}\quad f,g\in K^2_{\theta} \,\text{ such that }\ zf,zg\in K^2_{\theta}\end{align} $$

and called this property shift-invariance. In [17], this characterization was extended to the asymmetric case.

Example 2.9 Let $\alpha , \theta $ be nonconstant inner functions. Assume that $\mathcal {H}=\mathcal {K}=L^2$ , $H={K^2_{\alpha }}$ , $K={K^2_{\theta }}$ and $X=M_z$ , $Y=M_{\bar z}$ . Then condition (2) in Proposition 2.5 is the same as condition (2.9) (case $\theta =\alpha $ ). Thus an operator $A\in \mathcal {B}({K^2_{\alpha }},{K^2_{\theta }})$ is an asymmetric truncated Toeplitz operator if and only if it is $(M_z, M_{\bar z})$ -invariant. In case $\theta =\alpha $ , $A\in \mathcal {B}({K^2_{\theta }})$ is a truncated Toeplitz operator if and only if it is $M_z$ -invariant.

Similarly to (2.6), it can be checked that each bounded asymmetric truncated Toeplitz operator $A^{\alpha ,\theta }_{\varphi }$ is $(M_{ z}, M_{\bar z})$ -invariant.

Example 2.10 Recall now the notion of (asymmetric) truncated Hankel operators [17]. Let $\varphi \in L^2$ . Define

(2.10) $$ \begin{align}B^{\alpha,\theta}_{\varphi} f=P_{\theta} J(\varphi f)\qquad\text{ for}\quad f\in K^2_{\alpha}\cap L^{\infty}.\end{align} $$

and assume that $B^{\alpha ,\theta }_{\varphi }$ can be extended to a bounded operator from $K^2_{\alpha }$ to $K^2_{\theta }$ . We skip the word “asymmetric” if $\alpha =\theta $ . To give one more example of definition (2.2), let us take $\mathcal {H}=\mathcal {K}=L^2$ , $H={K^2_{\alpha }}$ , $K={K^2_{\theta }}$ and $X=M_z$ , $Y=M_{ z}$ . It can be easily shown using [17, Proposition 4.2(b)] that an operator is an (asymmetric) truncated Hankel operator if and only if it is $(M_{ z}, M_z)$ -invariant.

We will be particularly interested in compressions of multiplication operators to several closed subspaces of $\mathcal {H}=L^2$ . If $H, K\subset L^2$ are closed and $\varphi \in L^{\infty }$ , let

$$ \begin{align*} T_{\varphi}^{H, K}=P_K M_{\varphi} P_H|_{H}. \end{align*} $$

If $K=H$ , we write $T_{\varphi }^{H}$ . These are particular cases of the so-called general Wiener–Hopf operators [1, 13, 31], which we call general Toeplitz operators [6].

Proposition 2.11 Let $X\in \mathcal {B}(L^2)$ , and let $H, K$ be closed subspaces of $L^2$ . Then $ T_{\varphi }^{H, K}$ is X-invariant, whenever X commutes with multiplication by $\varphi $ in $L^2$ .

Proof Let $f\in H_X, g\in K_{X^*}$ . Then

$$ \begin{align*}\langle T_{\varphi}^{H, K} Xf,g\rangle = \langle P_K \varphi Xf,g\rangle = \langle \varphi Xf,g\rangle.\end{align*} $$

On the other hand,

$$ \begin{align*}\langle X\varphi f,g\rangle =\langle \varphi f,X^*g\rangle= \langle P_K \varphi f,X^*g\rangle=\langle T_{\varphi}^{H, K} f,X^*g\rangle.\\[-35pt]\end{align*} $$

Corollary 2.12 Let $H, K$ be closed subspaces of $L^2$ . Then $ T_{\varphi }^{H, K}$ is $M_{\psi }$ -invariant for all $\psi \in L^{\infty }$ . In particular, all compressions of a multiplication operator $M_{\varphi }$ to a closed subspace of $L^2$ are shift-invariant.

3 Invariance and preannihilator

In this section, we will consider $(X, Y)$ -invariance from a different point of view. For that we use the language of preannihilators and rank-one and rank-two operators in the preannihilator. Let $\mathcal {H}$ , $\mathcal {K}$ be separable Hilbert spaces. Each rank-one operator from $\mathcal {K}$ to $\mathcal {H}$ is usually denoted by $x\otimes y$ , where $x\in \mathcal {H}$ , $y\in \mathcal {K}$ , and it acts as $(x\otimes y)h=\langle h,y\rangle x$ for $h\in \mathcal {K}$ . The weak* topology (ultraweak topology) in $\mathcal {B}(\mathcal {H},\mathcal {K})$ is given by trace class operators of the form $t=\sum _{n=0}^{\infty } x_n\otimes y_n$ with $x_n\in \mathcal {H}$ , $y_n\in \mathcal {K}$ such that $\sum _{n=0}^{\infty } \|x_n\|^2< \infty $ , $\sum _{n=0}^{\infty } \|y_n\|^2< \infty $ . Let $\mathcal {B}_1(\mathcal {K},\mathcal {H})$ denote the space of all such trace class operators and $\|\cdot \|_1$ be the trace norm. Denote also by $\mathcal {F}_k$ the set of all operators in $\mathcal {B}_1(\mathcal {K},\mathcal {H})$ of rank at most k. Note that $\mathcal {B}(\mathcal {H},\mathcal {K})$ is a dual space to $\mathcal {B}_1(\mathcal {K},\mathcal {H})$ (see [24, Chapter 16] for details) and the dual action is given by

$$\begin{align*}\mathcal{B}(\mathcal{H},\mathcal{K})\ \times \ \mathcal{B}_1(\mathcal{K},\mathcal{H})\ni(T,t)\ \mapsto\ <T,t>=\sum_{n=0}^{\infty} \langle Tx_n,y_n\rangle.\end{align*}$$

For a closed subspace $\mathcal {S}\subset \mathcal {B}(\mathcal {H},\mathcal {K})$ , the preannihilator of $\mathcal {S}$ is defined as

$$\begin{align*}\mathcal{S}_{\perp}=\{t\in B_1(\mathcal{K},\mathcal{H})\colon <T,t>=0 \text{ for all } T\in\mathcal{S} \}.\end{align*}$$

Let $\mathcal {N}\subset \mathcal {B}_1(\mathcal {K},\mathcal {H})$ . Recall that the annihilator of $\mathcal {N}$ is given by

$$ \begin{align*}\mathcal{N}^{\bot}=\{T\in \mathcal{B}(\mathcal{H},\mathcal{K})\colon <T,t>=0 \text{ for all } t\in \mathcal{N} \}.\end{align*} $$

We will usually write, for $T\in \mathcal {B}(\mathcal {H}, \mathcal {K})$ and $t\in \mathcal {B}_1(\mathcal {K},\mathcal {H})$ , that $T\perp t$ if and only if $<T,t>=0$ . Note that $\mathcal {S}\subset \mathcal {B}(\mathcal {H},\mathcal {K})$ is weak*-closed if and only if $\mathcal {S} = (\mathcal {S}_{\perp })^{\perp }$ . Recall after [21] that a weak ${}^*$ -closed subspace $\mathcal {S}\subset \mathcal {B}(\mathcal {H},\mathcal {K}) $ is called k-reflexive ( $k=1, 2,3,4\dots $ ), if $\mathcal {S}=\big (\mathcal {S}_{\bot }\cap \mathcal {F}_k\big )^{\perp }$ .

Now we recall previous definitions (Definitions 1.2–1.4) from this perspective.

Proposition 3.1 Let $\mathcal {L},H $ be subspaces of a Hilbert space $\mathcal {H}$ such that $\mathcal {L}\subset H\subset \mathcal {H}$ , and let $X\in \mathcal {B}(\mathcal {H})$ . Then:

1. (1) $\mathcal {L}$ is invariant for X if and only if

   (3.1) $$ \begin{align} X\perp x\otimes y \qquad\text{for all}\quad x\in\mathcal{L},\ y\in \mathcal{H}\ominus\mathcal{L}. \end{align} $$

2. (2) $\mathcal {L}$ is almost-invariant for X if and only if there exists a finite dimensional subspace $\mathcal {F}$ such that

   (3.2) $$ \begin{align} X\perp x\otimes y \qquad\text{for all}\quad x\in\mathcal{L},\ y\in \mathcal{H}\ominus \big(\mathcal{L}\oplus \mathcal {F}\big). \end{align} $$

3. (3) $\mathcal {L}$ is nearly invariant for X with respect to H if and only if

   (3.3) $$ \begin{align} X\perp x\otimes y \qquad\text{for all}\quad x\in\mathcal{L}\cap H_X,\ y\in H\ominus\mathcal{L}. \end{align} $$

4. (4) $\mathcal {L}$ is nearly invariant for X with respect to H with defect m if and only if there exists a finite dimensional subspace $\mathcal {F}\subset H$ such that

   (3.4) $$ \begin{align} X\perp x\otimes y \qquad\text{for all}\quad x\in\mathcal{L}\cap H_X,\ y\in H\ominus\big(\mathcal{L}\oplus \mathcal{F}\big ), \end{align} $$

   where m is the smallest dimension of such subspace $\mathcal {F}$ .

Now we present a result concerning the topological behavior of the subspace of all $(X,Y)$ -invariant operators.

Proposition 3.2 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Then

$$\begin{align*}\mathcal{S}(X,Y)=\{A\in \mathcal{B}(H,K)\colon A \text{ is } (X,Y)\text{-invariant}\}\end{align*}$$

is $2$ -reflexive.

Proof Note that for $A\in \mathcal {B}(H,K)$ condition (2.2) is equivalent to

(3.5) $$ \begin{align} <A, Xf\otimes g-f\otimes Yg>=0\qquad \text{for}\qquad f\in H_X, g\in K_Y. \end{align} $$

Let us denote

(3.6) $$ \begin{align} \mathcal{N}=\Big\{Xf\otimes g-f\otimes Yg\colon\ f\in H_X, g\in K_Y \Big\}. \end{align} $$

By (3.5), we have

(3.7) $$ \begin{align} \mathcal{S}(X,Y)_{\perp}\supset \mathcal{N}\quad\quad\text{and }\quad\quad{\mathcal{S}(X,Y)}\supset \mathcal{N}^{\perp}. \end{align} $$

Thus

$$ \begin{align*}(\mathcal{S}(X,Y)_{\perp})^{\perp}\subset \mathcal{N}^{\perp}\subset \mathcal{S}(X,Y).\end{align*} $$

Hence, $\mathcal {S}(X,Y)$ is weak*-closed (WOT-closed), since it is characterized by annihilating some trace class (finite rank) operators. Moreover, $\mathcal {S}(X,Y)$ is $2$ -reflexive because

$$ \begin{align*} \Big(\mathcal{S}(X,Y)_{\perp} \cap \mathcal{F}_2\Big)^{\perp}\subset\Big(\mathcal{N}\cap\mathcal{F}_2\Big)^{\perp}=\mathcal{N}^{\perp}\subset\mathcal{S}(X,Y).\\[-37pt] \end{align*} $$

4 Kernels of $(X, Y)$ -invariant operators

It is a well-known property that kernels of Toeplitz operators are nearly $S^*$ -invariant. It was also proved in a recent paper [27] that kernels of truncated Toeplitz operators are nearly $S^*$ -invariant with defect not greater than $1$ . More generally, in this section, we study the invariance properties of the kernels of $(X,Y)$ -invariant operators.

One may look at the property of near X-invariance of a space $\mathcal {L}\subset H$ as meaning that, for any element $f\in \mathcal {L}$ , either $Xf$ is also in $\mathcal {L}$ , or it does not belong to H. In other words, looking at how X acts on elements of $\mathcal {L}$ , we see that either $(i) \; Xf\in \mathcal {L}$ , or $(ii)\, Xf\in H\setminus \mathcal {L}$ , or $(iii)\, Xf\in \mathcal {H}\setminus H$ ; if $\mathcal {L}$ is nearly X-invariant, then only $(i)$ and $(iii)$ can hold.

It is thus natural to ask, when $\mathcal {L}=\ker A$ , where $A\in \mathcal {B}(H, K)$ , for which elements $f\in \ker A$ does each of the properties $(i)$ – $(iii)$ hold.

On may also consider the question of describing the part $\mathcal {L}$ of $\ker A$ such that $X^*\mathcal {L}\subset \ker A$ , or $X^*\mathcal {L}\subset H$ , and compare with the analog results for X. Indeed, these questions are related, since we have, for co-isometric X,

(4.1) $$ \begin{align} (\ker A)_{X^*}\subset X(\ker A)_X. \end{align} $$

To see this note that, by (2.4), $f\in (\ker A)_{X^*}$ if and only if $X^*f\in (\ker A)_X$ . It follows that $f=XX^*f\in X(\ker A)_X$ . Note also that if X is unitary, then

$$ \begin{align*}(\ker A)_{X^*}= X(\ker A)_X.\end{align*} $$

Our first result is a very simple but fundamental one, when considering those questions. Let $ (\mathcal {L})_{H}^{\bot }=H\ominus \mathcal {L}$ for any closed subset $\mathcal {L}\subset H$ .

We have the following.

Proposition 4.1 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ . Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . If A is $(X,Y)$ -invariant, then

$$ \begin{align*} AXf\in (K_{Y})_K^{\bot} \quad \text{for all}\quad f\in \ker A\cap H_X. \end{align*} $$

Proof If $f\in \ker A$ and $Xf\in H$ , then, for all $g\in K_Y$ ,

$$ \begin{align*} \langle AXf,g\rangle = \langle Af,Yg\rangle=0, \quad \text{since}\quad Af=0.\\[-32pt] \end{align*} $$

As a consequence, we obtain the following necessary and sufficient condition for $\ker A$ to be nearly X-invariant.

Theorem 4.2 Let $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ , $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Assume that A is $(X,Y)$ -invariant. Then $ \ker A$ is nearly $X $ -invariant w.r.t. H if and only if $ AXf \in K_Y$ for all $ f\in \ker A\cap H_{X}$ .

Proof The space $\ker A$ is nearly X-invariant (in H) if and only if $AXf=0$ for all $f\in \ker A\cap H_X$ . Since $AXf\in (K_Y)_K^{\bot }$ , by Proposition 4.1, it will be zero if and only if $AXf\in K_Y$ .

Corollary 4.3 If A is $(X,Y)$ -invariant and $K_Y=K$ , then $\ker A$ is nearly X-invariant w.r.t. H.

Theorem 4.4 Let $H\subset \mathcal {H}$ and $K\subset \mathcal {K}$ , and let $A\in \mathcal {B}(H,K)$ , $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ . Assume that A is $(X,Y)$ -invariant. If $(K_Y)_K^{\bot }$ is finite dimensional, with dimension N, then $\ker A$ is nearly X-invariant w.r.t. H with defect $m\leqslant N$ .

Proof If $AXf\in K_Y$ for all $f \in \ker A\cap H_X$ , then by Proposition 4.1, we have $AXf=0$ for all $ f\in \ker A\cap H_{X}$ and $\ker A$ is nearly X-invariant w.r.t. H. Suppose now that there is $\tilde f\in \ker A\cap H_X$ with $AX\tilde f\notin K_Y$ (therefore, we necessarily have $AX\tilde {f}\neq 0$ , i.e., $X\tilde {f}\notin \ker A$ ). Define

$$ \begin{align*} \mathcal{I}=\{g\in (K_Y)_K^{\bot} : g=AXf \;\;\text{for same} \;\; f\in \ker A\cap H_X\}. \end{align*} $$

We have $\mathcal {I}\neq \{0\}$ because $AX\tilde f\neq 0$ and $AX\tilde f\in (K_Y)_K^{\bot }$ by Proposition 4.1. So let $\{g_1,g_2,\dots ,g_m\}$ , with $m\leqslant N$ , be a basis for $\mathcal {I}$ . For each $g_j$ , $j=1,2,\dots ,m$ , let $f_j$ be an element of $\ker A \cap H_X$ such that $g_j=AXf_j$ . We have that

$$ \begin{align*} A^{-1}\{g_j\}:=\{f\in H : Af=g_j\}=\{Xf_j+h\colon h\in \ker A\}. \end{align*} $$

Now take $h_j=(I-P_{\ker A})Xf_j\in A^{-1}\{g_j\}$ , which is such that $Ah_j=g_j$ and $h_j\in H \ominus \ker A$ . Then, for any $f\in \ker A\cap H_X$ , we have

$$ \begin{align*} AXf=\sum_{j=1}^mc_jg_j=\sum_{j=1}^m(c_jAh_j)=A\left(\sum_{j=1}^mc_jh_j\right), \end{align*} $$

with $c_j\in \mathbb {C}$ . Hence,

$$ \begin{align*} Xf-\sum_{j=1}^m c_jh_j \in \ker A \end{align*} $$

and we can write that

$$ \begin{align*} Xf\in \ker A\oplus \operatorname{\mathrm{span}}\{h_j\colon j=1,2,\dots,m\}.\\[-34pt] \end{align*} $$

Remark 4.5 From now on, we will use the notation

$$ \begin{align*} [h_j]_{j=1,\dots,m}:=\operatorname{\mathrm{span}}\{h_j \colon j=1,\dots,m\}. \end{align*} $$

We also define

$$ \begin{align*} H_X^A=\ker A\cap H_X. \end{align*} $$

Corollary 4.6 Let A be $(X,Y)$ -invariant. If $(K_Y)_K^{\bot }=[f_{Y}]$ for some $f_{Y}\in K$ , then $\ker A$ is nearly X-invariant w.r.t. H if and only if $AXf \bot f_{Y}$ for all $f\in H^A_X$ . Otherwise $\ker A$ is nearly X-invariant w.r.t. H with defect $1$ and, if $f_0$ is the element of $H_X^A$ such that $AXf_0=f_Y$ , then the defect space is $[h_0]$ with $h_0=(I-P_{\ker A})Xf_0$ .

Two simple examples illustrate these results.

Example 4.7 Let A be a Toeplitz operator ( $\mathcal {H}=\mathcal {K}=L^2$ , $H=K=H^2$ ) and take $X=M_{\bar z}$ , $Y=M_{z}$ ; we have $K_Y=(H^2)_{M_z}=H^2$ so, by (2.6) and Corollary 4.3, $\ker A$ is nearly $M_{\bar z}$ -invariant w.r.t. $H^2$ .

Taking $X=M_z$ , $Y=M_{\bar z}$ , we have $ (K_Y)^{\bot }=\mathbb {C}$ and it is easy to see that, for a Toeplitz operator $T_G$ with nontrivial kernel, there is always $f_0\in \ker T_G$ such that $T_Gzf_0=1$ . So we conclude from Corollary 4.6 that nontrivial Toeplitz kernels are nearly S-invariant with defect $1$ and thus also almost-invariant for $M_z$ with defect $1$ , at most (see Remark 1.5). These are in fact well-known properties that illustrate Proposition 2.2 in [11], stating that nearly $S^*$ -invariant spaces of the form $gK_I$ , as in Hitt’s theorem where $K=K_I$ is a model space, are almost-invariant for S with defect $1$ .

Example 4.8 Let A be an asymmetric truncated Toeplitz operator between model spaces $H={K^2_{\alpha }}$ , $K={K^2_{\theta }}$ , with $\alpha $ , $\theta $ nonconstant inner functions, and let $X=M_{\bar z}$ , $Y=M_{z}$ . Then $(K_Y)^{\bot }_K=(({K^2_{\theta }})_{M_z})^{\bot }_{K^2_{\theta }}=[\tilde k_0^{\theta }]$ , with $\tilde k_0^{\theta }=\bar z(\theta -\theta (0))$ ; so, by Example 2.9 and Corollary 4.6, kernels of (asymmetric) truncated Toeplitz operators are nearly $S^*$ -invariant with defect $1$ , at most (see also [27], Section 4 for the symmetric case).

5 Orthogonal decompositions of kernels

The study of near invariance properties for kernels of operators raises some natural questions. For instance, if $\ker A$ is nearly X-invariant w.r.t. H, which elements are kept in $\ker A$ under the action of X? If $\ker A$ is nearly X-invariant w.r.t. H with defect, which elements “stay” in H upon the action of X?

In this section, we show that the relations between $(X,Y)$ -invariance of an operator A and the near invariance properties of its kernel, with respect to X and Y, yield decompositions of the kernel in terms of orthogonal sums where the terms behave differently under the action of X. These decompositions generalize well-known decompositions of model spaces, such as those presented in the introduction.

To motivate the results that follow, we present two simple examples.

Example 5.1 (Model spaces)

Let $\theta $ be an inner function and assume, to begin with, that $\theta (0)=0$ . In this case, we have two decompositions

(5.1) $$ \begin{align} {K^2_{\theta}}=zK^2_{\frac{\theta}{z}}\oplus \mathbb{C}, \quad {K^2_{\theta}}=K^2_{\frac{\theta}{z}}\oplus \tfrac{\theta}{z}\mathbb{C}, \end{align} $$

where $\mathbb {C}=K^2_z$ . If $\theta (0)\neq 0$ , ${K^2_{\theta }}$ cannot be decomposed similarly in terms of $K^2_z$ and $K^2_{\frac {\theta }{z}}$ , but taking into account that ${K^2_{\theta }}=\ker T_{\bar \theta }$ and $K^2_{\frac {\theta }{z}}=\ker T_{\bar \theta z}$ , we can generalize (5.1) by writing

(5.2) $$ \begin{align} {K^2_{\theta}}&=z\ker T_{z\bar\theta}\oplus [k_0^{\theta}]=({K^2_{\theta}})_{\bar z}\oplus [k_0^{\theta}],\\ {K^2_{\theta}}&=\ker T_{z\bar\theta}\oplus [\tilde k_0^{\theta}]=({K^2_{\theta}})_z\oplus [\tilde k_0^{\theta}]\notag \end{align} $$

with

(5.3) $$ \begin{align} k_0^{\theta}=1-\overline{\theta(0)}\theta, \quad \tilde k_0^{\theta}=\bar z (\theta-\theta(0)). \end{align} $$

From the first decomposition in (5.2), we see that $\bar zK^2_{\theta }\subset K^2_{\theta } \oplus [\bar z]$ and

$$ \begin{align*} M_{\bar z}(z\ker T_{z\bar\theta})\subset {K^2_{\theta}}, \quad M_{\bar z}(k_0^{\theta})\in L^2\setminus H^2, \end{align*} $$

which reflects the fact that ${K^2_{\theta }}$ is nearly $M_{\bar z}$ -invariant w.r.t. $H^2$ .

From the second decomposition in (5.2), we see that $ zK^2_{\theta }\subset K^2_{\theta } \oplus [\theta ]$ (cf. [11], Proposition 2.2) and

$$ \begin{align*} M_z(\ker T_{z\bar\theta})\subset {K^2_{\theta}}, \quad M_z(\tilde k_0^{\theta})\in H^2\setminus {K^2_{\theta}}, \end{align*} $$

so we may interpret it as saying that ${K^2_{\theta }}$ is $H^2$ -invariant for $M_z$ and nearly S-invariant with defect $1$ , w.r.t. $H^2$ , therefore almost-invariant for S with defect $1$ .

These are well-known properties; still, they provide an interpretation of the equalities in (5.2) which will lead to future results generalizing model space decompositions.

Example 5.2 (Kernels of truncated Toeplitz operators on ${K^2_{\theta }}$ with analytic symbols)

The kernels of operators in this class are of the form $\gamma {K^2_{\beta }}$ , where $\gamma $ and $\beta $ are inner functions such that $\beta \leqslant \theta $ , $\gamma =\theta /\beta $ and $\beta $ divides $\psi _+^i$ -the inner factor of $\psi _+$ , [26], [10, Theorem 7.2]. Let A be a truncated Toeplitz operator with $\ker A=\gamma {K^2_{\beta }}$ . Then, from (5.2), we have

(5.4) $$ \begin{align} \ker A=\gamma({K^2_{\beta}})_{\bar z}\oplus[\gamma k_0^{\beta}] \quad \text{with} \quad (\ker A)_{\bar z}=\gamma ({K^2_{\beta}})_{\bar z}. \end{align} $$

Let us assume that $\gamma (0)=0$ , in which case $\gamma {K^2_{\beta }}$ is not nearly $S^*$ -invariant. Note that, since $\gamma (0)=0$ , both terms of the orthogonal sum are mapped into $H^2$ by multiplication by $\bar z$ . On the other hand, only the elements of $(\ker A)_{\bar z}$ are mapped into $\ker A$ . We thus conclude that $\ker A$ is almost $S^*$ -invariant (or, equivalently, almost $S_{\theta }$ -invariant, where $S_{\theta }=A^{\theta }_z$ is the truncated shift) with defect $1$ and defect space $[\bar z\gamma k_0^{\beta }]$ .

These decompositions of the kernels of certain operators, in terms of direct sums of subspaces behaving in different ways under multiplication by z and $\bar z$ , can be seen as resulting from the relation between the shift-invariance of the operator and the invariance properties of their kernels, as we show next.

Recall that for $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $H\subset \mathcal {H}$ ,

(5.5) $$ \begin{align} H_{ X}^A=\ker A\cap H_X. \end{align} $$

Proposition 5.3 Let $A\in \mathcal {B}(H,K)$ and $X\in \mathcal {B}(\mathcal {H})$ , $H\subset \mathcal {H}$ . Then

$$ \begin{align*}\ker A=H_{ X}^A\oplus P_{\ker A}\, H_X^{\bot}.\end{align*} $$

Proof We have to prove that $H_{ X}^A$ is the orthogonal complement of $P_{\ker A}\,H_X^{\bot }$ in $\ker A$ . Let $f\in \ker A$ , $f \bot P_{\ker A}H_X^{\bot }$ . Then $f\bot H_X^{\bot }$ and so $f\in \ker A\cap H_X=H_{ X}^A$ .

Conversely, if $f\in H_{ X}^A$ , then, for all $g\in H_X^{\bot }$ ,

$$ \begin{align*} \langle f,P_{\ker A}\,g \rangle = \langle f, g\rangle=0 \end{align*} $$

because $f\in H_X$ and $g\in H_X^{\bot }$ .

Recall that

$$ \begin{align*} (\ker A)_X=\{f\in \ker A : Xf\in \ker A\}\subset H_{ X}^A. \end{align*} $$

In its turn, we can decompose $H_{ X}^A$ as follows.

Proposition 5.4 Let $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ , $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ . If $A\in \mathcal {B}(H,K)$ is $(X,Y)$ -invariant, then

$$ \begin{align*} H_{ X}^A=(\ker A)_X\oplus P_{H^A_X}(X^*A^* K_Y^{\bot}), \end{align*} $$

where we abbreviate $(K_Y)^{\bot }_K$ to $K_Y^{\bot }$ .

Proof Let $f\in (\ker A)_X$ . Then obviously $AXf=0$ , and hence, for all $g\in K_Y^{\bot }$ , we have

$$ \begin{align*} 0=\langle AXf,g\rangle = \langle Xf,A^*g\rangle =\langle f, X^*A^*g\rangle= \langle f,P_{H_{ X}^A} (X^*A^*g)\rangle. \end{align*} $$

Therefore, $f\bot P_{H_{ X}^A}(X^*A^* K_Y^{\bot })$ for all $f\in (\ker A)_X$ . Conversely, let $f\in H_X^A$ and

(5.6) $$ \begin{align} f\bot P_{H_{ X}^A}(X^*A^* K_Y^{\bot}). \end{align} $$

For all $g\in K_{Y}$ , we have, by (2.2), $0=\langle AXf,g\rangle =\langle Af, Yg\rangle $ so

$$ \begin{align*} 0=\langle Xf,A^*g\rangle =\langle f, X^*A^*g\rangle =\langle f,P_{H^A_X} (X^*A^*g)\rangle. \end{align*} $$

Hence,

(5.7) $$ \begin{align} f\bot P_{H^A_X} (X^*A^* K_{Y}). \end{align} $$

From (5.6) and (5.7), we conclude that, for $f\in (\ker A)_X$ , $f\bot P_{H^A_X}( X^*A^*K)$ , so for all $g\in K$ , we have

$$ \begin{align*} 0=\langle f,P_{H^A_X} (X^*A^*g)\rangle = \langle f, X^*A^*g\rangle = \langle AXf,g\rangle, \end{align*} $$

and hence $AXf=0$ , so $Xf\in \ker A$ and thus $f\in (\ker A)_X$ .

Clearly, $\ker A$ is nearly X-invariant w.r.t. H if and only if $H_{ X}^A=(\ker A)_X$ , so we have the following.

Corollary 5.5 Let $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ , $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ . Assume that $A\in \mathcal {B}(H,K)$ is $(X,Y)$ -invariant. Then the subspace $\ker A$ is nearly X-invariant w.r.t. H if and only if $P_{H_{ X}^A}(X^*A^* K_Y^{\bot })=\{0\}$ , i.e., $\langle AXf,g\rangle =0$ for all $f\in H^A_X$ , $g\in K_Y^{\bot }$ .

The subspace $\ker A$ is nearly X-invariant w.r.t. H with defect if and only if

(5.8) $$ \begin{align} \dim P_{H_{ X}^A}(X^*A^*K_{Y}^{\bot})<\infty. \end{align} $$

As a consequence of the previous results, we have the following.

Theorem 5.6 Let $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ , $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ . If $A\in \mathcal {B}(H,K)$ is $(X,Y)$ -invariant, then we have the orthogonal decomposition

(5.9) $$ \begin{align}\ker A=(\ker A)_X \oplus P_{H_{ X}^A}( X^* A^* K_Y^{\bot})\oplus P_{\ker A}H_X^{\bot}. \end{align} $$

Moreover, if X, Y are co-isometries, then A is $(X^*,Y^*)$ -invariant, and we have

(5.10) $$ \begin{align}\ker A=(\ker A)_{X^*} \oplus P_{H^A_{X^*}}( X A^* K_{Y^*}^{\bot})\oplus P_{\ker A}H_{X^*}^{\bot}. \end{align} $$

Corollary 5.7 Let $X\in \mathcal {B}(\mathcal {H})$ , $H\subset \mathcal {H}$ . If $A\in \mathcal {B}(H)$ is X-invariant, then we have the orthogonal decomposition

(5.11) $$ \begin{align}\ker A=(\ker A)_X \oplus P_{H_{ X}^A}( X^* A^* H_{X^*}^{\bot})\oplus P_{\ker A}H_X^{\bot}. \end{align} $$

Moreover, if X is a co-isometry, then A is $X^*$ -invariant, and we have

(5.12) $$ \begin{align}\ker A=(\ker A)_{X^*} \oplus P_{H^A_{X^*}}( X A^* H_{X}^{\bot})\oplus P_{\ker A}H_{X^*}^{\bot}. \end{align} $$

Remark 5.8 In (5.9), we have that $(\ker A)_X$ consists of the elements of $\ker A$ which are mapped into $\ker A$ by X;

(5.13) $$ \begin{align} M_A^{\prime}(X):=P_{H_{ X}^A}(X^*A^* K_Y^{\bot}) \end{align} $$

consists of elements which are mapped into $H \setminus \ker A$ by X; and

(5.14) $$ \begin{align} M_A^{\prime\prime}(X):=P_{\ker A}H_{X}^{\bot} \end{align} $$

consists of elements which are mapped into $\mathcal {H}\setminus H$ by X.

Similarly, having (5.10), we can consider the following spaces:

(5.15) $$ \begin{align}(\ker A)_{X^*};\quad M_A^{\prime}(X^*):=P_{H_{ X}^A}(XA^* K_{Y^*}^{\bot});\quad M_A^{\prime\prime}(X^*):=P_{\ker A}H_{X^*}^{\bot}. \end{align} $$

According to definitions (5.13) and (5.14), we have the following.

Corollary 5.9 Let $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ , $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ . If $A\in \mathcal {B}(H,K)$ is $(X,Y)$ -invariant, then:

1. (1) $\ker A \cap H_X=H_{ X}^A=(\ker A)_X\oplus M_A^{\prime }(X)$ .

2. (2) $\ker A$ is nearly X-invariant w.r.t. H if and only if $M_A^{\prime }(X)=\{0\}$ .

3. (3) If $\dim M_A^{\prime }(X)<\infty $ , $\ker A$ is nearly X-invariant with defect.

4. (4) $M_A^{\prime \prime }(X)=\{0\}$ if and only if $X(\ker A)\subset H$ , i.e., $\ker A$ is almost-invariant for X.

5. (5) $\ker A$ is almost-invariant for $\tilde X=P_{H}X|_{H}$ if $M_A^{\prime \prime }(X)=\{0\}$ , $\dim M_A^{\prime }(X)<\infty $ .

Corollary 5.10 Let $X\in \mathcal {B}(\mathcal {H})$ , $Y\in \mathcal {B}(\mathcal {K})$ , $H\subset \mathcal {H}$ , $K\subset \mathcal {K}$ . Assume that $A\in \mathcal {B}(H,K)$ is $(X,Y)$ -invariant. If $K_Y^{\bot }=\big [f_Y\big ]$ , $H_X^{\bot }=\big [f_{X}\big ]$ , then

$$ \begin{align*} \ker A=(\ker A)_X \oplus \big [P_{H_{ X}^A}( X^* A^*f_{ Y})\big]\oplus\big[ P_{\ker A}f_X\big]. \end{align*} $$

In this case, $\ker A$ is nearly X-invariant with defect at most $1$ .

Remark 5.11 With the same assumptions as in Corollary 5.10 and taking Corollary 5.9(1) into account, we have, for $f\in H_{ X}^A$ ,

$$ \begin{align*} Xf\in X(\ker A)_X \oplus [XP_{H_{ X}^A}(X^*A^*f_{Y})], \end{align*} $$

where the direct sum is orthogonal if X is unitary, and the second term in the sum gives the defect space for the near X-invariance of $\ker A$ .

We finish this section by establishing a relation between X-invariance and conjugations that will be used later. Recall that by a conjugation on $\mathcal {H}$ , we mean an antilinear operator which is involutive and isometric [16].

Proposition 5.12 Let C be a conjugation on $\mathcal {H}$ , and let $H \subset \mathcal {H}$ be a Hilbert space. If $C(H)=H$ and $X\in \mathcal {B}(\mathcal {H})$ is such that $C X^*=XC$ , then $C(H_X)=H_{X^*}$ .

Proof Let $f\in H$ , $Xf\in H$ . Then $C f\in H$ and $X^* C f=C Xf\in H$ .

6 Toeplitz operators

Now we apply the previous results to kernels of Toeplitz operators. In what follows, we assume that $G \in L^{\infty }$ and $T_G\colon H^2\to H^2$ is defined by $T_Gf=P^+Gf$ for all $f\in H^2$ , where $P^+$ is the orthogonal projection from $L^2$ onto $H^2$ . Since, for any nonzero Toeplitz kernel strictly contained in $H^2$ , one can associate a unimodular symbol [8, 29], we may assume that $|G|=1$ . We assume also that $\ker T_G\neq \{0\}$ . We have the following [8, 23].

Proposition 6.1 Let $G\in L^{\infty }$ . For $|G|=1$ , we have $\ker T_G\neq \{0\}$ if and only if G admits a factorization of the form $G=\overline {O_+}\bar z\bar I O_+^{-1}$ , where I is an inner function, $O_+\in H^2$ is outer.

Since the existence of a factorization such as described in Proposition 6.1 is in general difficult to verify, unless G belongs to some special class such as that of nonvanishing piecewise continuous functions on the unit circle $\mathbb {T}$ [25], one may alternatively consider the Riemann–Hilbert problem

(6.1) $$ \begin{align} Gf_+=f_- \quad \text{with}\quad f_+\in H^2, \; f_-\in H^2_-:=\bar z \overline{H^2}. \end{align} $$

Indeed, $\ker T_G$ consist of all solutions $f_+$ to this problem, so $\ker T_G\neq \{0\}$ if and only if there exists a nonzero solution to (6.1) (which may be obtained using a variety of methods developed to solve Riemann–Hilbert problems).

Consider $\mathcal {H}=\mathcal {K}=L^2$ and let $X=M_{\beta }$ , or simply $X=\beta $ , with $\beta $ inner, and $Y=X^*$ . We have that $T_G$ is $\beta $ -invariant by Corollary 2.12 and, in this case,

(6.2) $$ \begin{align} H=H^2, \; H_X=(H^2)_{\beta}=H^2, \; H_{X^*}=(H^2)_{\bar\beta}=\beta H^2, \end{align} $$

(6.3) $$ \begin{align} H_X^{\bot}=\{0\}, \; H_{X^*}^{\bot}={K^2_{\beta}}. \end{align} $$

To apply the decomposition given in Theorem 5.6, we first describe the spaces $(\ker T_G)_{\beta }$ and $(\ker T_G)_{\bar \beta }$ .

Proposition 6.2 Let $\beta $ be an inner function, and let $G\in L^{\infty }$ . Then

$$ \begin{align*} (\ker T_G)_{\beta} = \ker T_{\beta G};\qquad\qquad (\ker T_G)_{\bar\beta}= \beta \ker T_{\beta G}. \end{align*} $$

Proof We have $\ker T_{\beta G}\subset \ker T_G$ , where the inclusion is strict if $\beta \notin \mathbb {C}$ . On the other hand, if $f\in \ker T_{\beta G}$ , then $\beta Gf=f_-\in H^2_-$ , so $G(\beta f)=f_-$ and it follows that $\beta f\in \ker T_G$ . Hence, $\ker T_{\beta G}\subset (\ker T_G)_{\beta }$ . Conversely, if $f\in (\ker T_G)_{\beta }$ , then $f, \beta f\in \ker T_G$ , so $G(\beta f)=f_-\in H^2_-$ , which is equivalent to $(\beta G)f=f_-$ , and thus $f\in \ker T_{\beta G}$ .

The second equality follows by (4.1).

Remark 6.3 The relations between $\ker T_G$ and $\ker T_{\beta G}$ were studied in [5] where it was shown, in particular, that $\ker T_{\beta G}=\{0\}$ if $\dim \ker T_G<\infty $ and $\dim {K^2_{\beta }} \geqslant \dim \ker T_G$ . However, it may be difficult to see whether or not $\ker T_{\beta G}=\{0\}$ when $\ker T_G$ is infinite dimensional and $\beta $ is not a finite Blaschke product (see, for instance, [5] for some examples).

The decomposition theorem now yields the following.

Theorem 6.4 Let $G\in L^{\infty }$ and $\beta $ be an inner function. The following orthogonal decompositions hold:

(6.4) $$ \begin{align} \ker T_G =\ker T_{\beta G}\oplus P_{\ker T_G}(\bar G\bar z\overline{{K^2_{\beta}}})=(H^2)_{\beta}^{ T_G}; \end{align} $$

(6.5) $$ \begin{align} \ker T_G =\beta \ker T_{\beta G}\oplus P_{\ker T_G}{K^2_{\beta}}. \end{align} $$

Proof The decompositions follow from Corollary 5.7, Propositions 5.4 and 6.2, and (6.2) and (6.3). For (6.4), we took into account that, for $A=T_G$ ,

$$\begin{align*}P_{{H_{\beta}^A}}(\bar\beta P^+\bar G {K^2_{\beta}})=P_{\ker A}(\bar\beta P^+\bar G {K^2_{\beta}})= P_{\ker T_G}(\bar\beta \bar G{K^2_{\beta}})\end{align*}$$

and $\bar \beta \bar G {K^2_{\beta }}= \bar G\bar z \overline {{K^2_{\beta }}}$ .

Remark 6.5 With the notation (5.13) and (5.14), we see that in (6.4), we have $M_A^{\prime \prime }(\beta )=\{0\}$ , which reflects the fact that $\beta \ker T_G\subset H^2$ . It also follows that $\ker T_G$ is almost-invariant for $M_{\beta }$ if $\beta $ is a finite Blaschke product. On the other hand, regarding (6.5), with $X=\bar \beta $ , one sees that $M_A^{\prime }(\bar \beta )=\{0\}$ which corresponds to $\ker T_G$ being nearly $\bar \beta $ -invariant.

Example 6.6 If $G=\bar \alpha $ , where $\alpha $ is an inner function, then $\ker T_G={K^2_{\alpha }}$ . If $\beta < \alpha $ , the decompositions (6.4) and (6.5) become

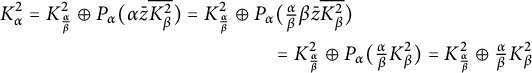$$ \begin{align*} {K^2_{\alpha}}=K^2_{\frac{\alpha}{\beta}}\oplus P_{\alpha}(\alpha\bar z \overline{{K^2_{\beta}}})=K^2_{\frac{\alpha}{\beta}} &\oplus P_{\alpha}(\tfrac{\alpha}{\beta} \beta \bar z \overline{{K^2_{\beta}}})\\ &\qquad =K^2_{\frac{\alpha}{\beta}}\oplus P_{\alpha}(\tfrac{\alpha}{\beta} {K^2_{\beta}})=K^2_{\frac{\alpha}{\beta}}\oplus \tfrac{\alpha}{\beta} {K^2_{\beta}} \end{align*} $$

and

$$ \begin{align*} {K^2_{\alpha}}=\beta K^2_{\frac{\alpha}{\beta}}\oplus P_{\alpha} {K^2_{\beta}}=\beta K^2_{\frac{\alpha}{\beta}}\oplus {K^2_{\beta}}, \end{align*} $$

and we recover the known decompositions for ${K^2_{\alpha }}$ ,

(6.6) $$ \begin{align} {K^2_{\alpha}}=K^2_{\frac{\alpha}{\beta}}\oplus \tfrac{\alpha}{\beta} {K^2_{\beta}}, \qquad {K^2_{\alpha}}=\beta K^2_{\frac{\alpha}{\beta}}\oplus {K^2_{\beta}}. \end{align} $$

Now consider, for a given inner function $\alpha $ , the usual conjugation $C_{\alpha }$ in $L^2$ given by $C_{\alpha } f=\alpha \bar z \bar f$ . This conjugation leaves the model space ${K^2_{\alpha }}$ invariant, i.e., $C_{\alpha } {K^2_{\alpha }}={K^2_{\alpha }}$ . Moreover, as shown in [4], it is the only (up to multiplication by a constant of modulus 1) conjugation C such that $CM_z=M_{\bar z}C$ and $C{K^2_{\alpha }}\subset {K^2_{\alpha }}$ . It is not difficult to see that this unique conjugation $C_{\alpha }$ maps the two decompositions (6.6) onto each other, i.e.,

(6.7) $$ \begin{align} C_{\alpha}(K^2_{\frac{\alpha}{\beta}})=\beta K^2_{\frac{\alpha}{\beta}}, \qquad C_{\alpha}(\tfrac{\alpha}{\beta} {K^2_{\beta}})={K^2_{\beta}}. \end{align} $$

Recently, in [14], it was shown that, for a given unimodular function G, the only (up to multiplication by a constant of modulus 1) conjugation C such that $CM_z=M_{\bar z}C$ and $C\ker T_G\subset \ker T_G$ has the form

(6.8) $$ \begin{align} C_Gf=\bar G\bar z\bar f, \; f\in L^2. \end{align} $$

Using this conjugation, the results in (6.7) may be generalized for all Toeplitz kernels as follows.

Proposition 6.7 Let $G\in L^{\infty }$ be a unimodular function, and let $C_G$ be the conjugation defined by (6.8). Then

(6.9) $$ \begin{align} {C}_G(\ker T_G)_{\bar\beta}=(\ker T_G)_{\beta}, \end{align} $$

(6.10) $$ \begin{align} {C}_G(P_{\ker T_G}{K^2_{\beta}})=P_{\ker T_G}({C}_G {K^2_{\beta}})=P_{\ker T_G}(\bar G\bar z \overline{{K^2_{\beta}}}). \end{align} $$

Proof The first equality is a consequence of Proposition 5.12, with $\mathcal {H}=\ker T_G$ , since ${C}_GM_{\bar \beta }=M_{\beta } {C}_G$ . The second equality is a consequence of ${C}_G$ being a conjugation on $\ker T_G$ .

We thus have, as it happened in the case of model spaces:

Corollary 6.8 The two decompositions in Theorem 6.4 are mapped into each other by the conjugation ${C}_G$ defined on $\ker T_G$ .

The following example also raises an interesting question.

Example 6.9 Let $|G|=1$ and take $\beta =z$ . If $G=\bar \theta $ , then $\ker T_G={K^2_{\theta }}$ . Since $P_{\theta } (\bar z\theta )=\tilde k_0^{\theta }$ , we have

(6.11) $$ \begin{align} {K^2_{\theta}}=\ker T_{z\bar\theta}\oplus [\tilde k_0^{\theta}]. \end{align} $$

In Example 6.9, $\tilde k_0^{\theta }$ is a maximal function for the Toeplitz kernel ${K^2_{\theta }}$ , i.e., it cannot belong to any Toeplitz kernel strictly contained in ${K^2_{\theta }}$ , such as $\ker T_{z\bar \theta }$ [7]. However, (6.11) tells us furthermore that there exists a maximal function for ${K^2_{\theta }}$ which is orthogonal to $\ker T_{z\bar \theta }=({K^2_{\theta }})_z$ .

This raises the following question: given any Toeplitz kernel, $\ker T_G$ , is there a maximal function which is orthogonal to $(\ker T_G)_z$ ? Since, from (6.4),

$$ \begin{align*} \ker T_G=(\ker T_G)_z \oplus [P_{\ker T_G}(\bar z\bar G)], \end{align*} $$

that question in equivalent to asking whether $P_{\ker T_G}(\bar z\bar G)$ is a maximal function for $\ker T_G$ .

It was shown in [7] that every Toeplitz kernel has a maximal function and, in [5, 8] that $f_M$ is a maximal function for $\ker T_G$ if and only if $Gf_M=\bar z\bar h$ , where $h\in H^2$ is outer. We have

$$ \begin{align*} P_{\ker T_G}(\bar z\bar G)=P_{\ker T_G}({C}_G1)={C}_G(P_{\ker T_G}1)=\bar z\bar G \overline{P_{\ker T_G}1} \end{align*} $$

and thus

$$ \begin{align*} GP_{\ker T_G}(\bar z\bar G)=\bar z \overline{P_{\ker T_G}1}. \end{align*} $$

Therefore, $P_{\ker T_G}(\bar z\bar G)$ is a maximal function for $\ker T_G$ if and only if $P_{\ker T_G}1$ is outer. Now, using Hitt’s/Hayashi’s representation $\ker T_G=g K_I$ (Theorem 1.1), where g is an outer function, and the expression for $P_{\ker T_G}$ given in [18], we have

$$ \begin{align*} P_{\ker T_G}1=gP_I\bar g\cdot 1 =gIP^-\bar IP^+\bar g=g \,\overline{g(0)}(1-\overline{I(0)}I) \end{align*} $$

which is outer, since $g(0)\neq 0$ . We have thus proved the following.

Proposition 6.10 Let $G\in L^{\infty }$ be a unimodular function. There exists a maximal function $f_M$ in $\ker T_G$ such that

$$ \begin{align*} \ker T_G=\ker T_{zG}\oplus [f_M]. \end{align*} $$

If $\ker T_G=g K_I$ is Hitt’s representation of $\ker T_G$ according to Theorem 1.1, then such a maximal function is given by

$$ \begin{align*} f_M=P_{\ker T_G}(\bar z\bar G) =\bar z\bar G \bar g\,g(0)(1-I(0)\bar I). \end{align*} $$

7 Truncated Toeplitz operators

Now we apply the previous results to truncated Toeplitz operators, for $X=\bar \beta $ and $X=\beta $ , identifying as before $M_{\alpha }$ with $\alpha $ , for $\alpha \in L^{\infty }$ .

Let $\theta ,\beta $ be nonconstant inner functions. Consider the model space $K^2_{\theta }\subset L^2$ and the operator $X=M_{\bar \beta }$ (we will simply write $X=\bar \beta $ ). Let $G\in L^{\infty }$ , and let $A_G^{\theta } \colon {K^2_{\theta }} \to {K^2_{\theta }}$ be defined by $A_G^{\theta } f=P_{\theta } Gf$ , $f\in {K^2_{\theta }}$ . In this case, we have $\mathcal {H}=L^2,\,H={K^2_{\theta }}$ and from Proposition 6.2 and Theorem 6.4,

(7.1) $$ \begin{align} H_{\beta}&=({K^2_{\theta}})_{\beta}=\ker T_{\beta \bar\theta}, \quad &(H_{\beta})_{K_{\theta}^2}^{\bot}= ({K^2_{\theta}})_{\beta}^{\bot}&=P_{\theta}(\theta\bar z\overline{{K^2_{\beta}}}), \end{align} $$

(7.2) $$ \begin{align} H_{\bar\beta}&=({K^2_{\theta}})_{\bar\beta}=\beta\ker T_{\beta \bar\theta}, \quad &(H_{\bar\beta})_{K_{\theta}^2}^{\bot}=({K^2_{\theta}})_{\bar\beta}^{\bot}&=P_{\theta}({K^2_{\beta}}), \end{align} $$

where we abbreviate, for $\alpha \in L^{\infty }$ , ${[(K_{\theta }^2)_{\alpha }}]^{\bot }_{K^2_{\theta }}$ to ${(K_{\theta }^2})^{\bot }_{\alpha }$ .

Two particular cases are worth mentioning. The first is the case where $({K^2_{\theta }})_{\beta }=\ker T_{\beta \bar \theta }=\{0\}$ , which was mentioned in Section 5. In this case, we have from Theorem 6.4 that $P_{\theta }(\theta \bar z\overline {{K^2_{\beta }}})=P_{\theta }(\theta \bar \beta {K^2_{\beta }})=K^2_{\theta } $ and $P_{\theta }({K^2_{\beta }})=K^2_{\theta }$ .

The second case is with $\beta <\theta $ , where

(7.3) $$ \begin{align}H_{\beta}&=({K^2_{\theta}})_{\beta}=K^2_{\frac{\theta}{\beta}}, & (H_{\beta})_{K_{\theta}^2}^{\bot}= ({K^2_{\theta}})_{\beta}^{\bot}&=\tfrac{\theta}{\beta}{K^2_{\beta}}, \end{align} $$

(7.4) $$ \begin{align} H_{\bar\beta}&=({K^2_{\theta}})_{\bar\beta}=\beta K^2_{\frac{\theta}{\beta}}, &(H_{\bar\beta})_{K_{\theta}^2}^{\bot} = ({K^2_{\theta}})_{\bar\beta}^{\bot} &={K^2_{\beta}}. \end{align} $$

In what follows, we will use the notation

(7.5) $$ \begin{align} (K^2_{\theta})^G_X= \ker A_G^{\theta}\cap(K^2_{\theta})_X. \end{align} $$

We start by applying Theorem 5.6 for $X=\bar \beta $ :

Theorem 7.1 Let $\theta ,\beta $ be nonconstant inner functions, and let $G\in L^{\infty }$ . Then

(7.6) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_{\bar\beta}\oplus M_G^{\prime}(\bar\beta)\oplus M_G^{\prime\prime}(\bar\beta), \end{align} $$

where

(7.7) $$ \begin{align} M_G^{\prime}(\bar\beta)&:=M_{A_G^{\theta}}^{\prime}(M_{\bar\beta})=P_{(K^2_{\theta})^G_{\bar\beta}}\,\,\beta A_{\bar G}^{\theta}( P^+(\theta \bar{\beta} K^2_{\beta})), \end{align} $$

(7.8) $$ \begin{align} M_G^{\prime\prime}(\bar\beta)&:=M_{A_G^{\theta}}^{\prime\prime}(M_{\bar\beta})= P_{\ker A_G^{\theta}}({K^2_{\beta}}), \end{align} $$

abbreviating $(K^2_{\theta })_{\beta }^{\perp }={K^2_{\theta }}\ominus ({K^2_{\theta }})_{\beta }$ and $(K^2_{\theta })_{\bar \beta }^{\perp }={K^2_{\theta }}\ominus ({K^2_{\theta }})_{\bar \beta }$ , respectively.

Remark 7.2 Note that $M_G^{\prime }(\bar \beta )$ , $M_G^{\prime \prime }(\bar \beta )$ cannot be zero simultaneously (when $\ker A_G^{\theta }$ is not zero). In that case $\ker A_G^{\theta }$ would be $\bar \beta $ -invariant and in consequence $\bar \beta \ker A_G^{\theta }\subset \ker A_G^{\theta }\subset H^2$ . That would give $\ker A_G^{\theta }\subset \beta \ker A_G^{\theta }$ , implying that $\ker A_G^{\theta }\subset \beta ^N H^2$ for any N, which is a contradiction.

Corollary 7.3 With the same assumptions and notation as in Theorem 7.1, the following are equivalent:

1. (1) $M_G^{\prime \prime }(\bar \beta )=\{0\}$ .

2. (2) $\ker A_G^{\theta }$ is $K^2_{\theta }$ -stable for $M_{\bar \beta }$ .

3. (3) $\ker A_G^{\theta }\subset \beta {K^2_{\theta }}\cap {K^2_{\theta }}=\beta \ker T_{\beta \bar \theta }=(K^2_{\theta })_{\bar \beta }$ .

4. (4) $\ker A_G^{\theta }=(\ker A_G^{\theta })_{\bar \beta }\oplus P_{\ker A_G^{\theta }}\,\,\beta A_{\bar G}^{\theta }( P^+(\theta \bar {\beta } K^2_{\beta }))$ .

Proof The equivalence $(1)\Leftrightarrow (2)$ is obvious. Regarding $(1)\Leftrightarrow (3)$ , we have that $P_{\ker A_G^{\theta }}({K^2_{\beta }})=\{0\}$ if and only if $P_{\ker A_G^{\theta }}(P_{\theta }{K^2_{\beta }})= P_{\ker A_G^{\theta }}({K^2_{\theta }})_{\bar \beta }^{\bot }=\{0\}$ , which is equivalent to $\ker A_G^{\theta }\subset ({K^2_{\theta }})_{\bar \beta }=\beta \ker T_{\beta \bar \theta }$ . In this case, we have $(K^2_{\theta })^G_{\bar \beta }=\ker A_G^{\theta } \cap (K^2_{\theta })_{\bar \beta }=\ker A_G^{\theta }$ , so the decomposition (4) follows from Theorem 7.1. Conversely, if (4) holds, then no element of $\ker A_G^{\theta }$ is mapped outside $\ker A_G^{\theta }$ by $M_{\bar \beta }$ , so (1) holds.

In the following corollary, note that saying that a closed subspace K of $K^2_{\theta }$ is nearly $S^*$ -invariant w.r.t. $H^2$ is equivalent to saying that K is nearly $S^*$ -invariant w.r.t. $K^2_{\theta }$ , since $K^2_{\theta }$ is itself nearly $S^*$ -invariant.

Corollary 7.4 With the same assumptions and notation as in Theorem 7.1, the following are equivalent:

1. (1) $ M_G^{\prime }(\bar \beta )=\{0\}$ .

2. (2) $ \ker A_G^{\theta }$ is nearly $\bar \beta $ -invariant (w.r.t. $H^2$ , w.r.t. $K^2_{\theta }$ ).

3. (3) $ A_G^{\theta }(\bar \beta f)\in ({K^2_{\theta }})_{\beta }= \ker T_{\beta \bar \theta }$ , for all $\;f\in (K^2_{\theta })_{\bar \beta }^{G}$ .

4. (4) $P_{\beta }(\bar \theta Gf)=0$ , for all $\;f\in (K^2_{\theta })_{\bar \beta }^{G}$ .

Proof The first equivalence is trivial. Note that $M_G^{\prime }(\bar \beta )=\{0\}$ if and only if $P_{(K^2_{\theta })_{\bar \beta }^{G}}(\beta A_{\bar G}^{\theta }(P^+ \theta \bar \beta {K^2_{\beta }}))=\{0\}$ . This is equivalent to the fact that, for all $h\in ({K^2_{\theta }})_{\beta }^{\bot }, \; f\in (K^2_{\theta })_{\bar \beta }^{G}$ , we have

$$\begin{align*}0=\langle \beta A_{\bar G}^{\theta} h,f\rangle =\langle h,A_G^{\theta}(\bar\beta f)\rangle,\end{align*}$$

that is, $ A_G^{\theta }(\bar \beta f)\in ({K^2_{\theta }})_{\beta }=\ker T_{\beta \bar \theta }$ . So the second equivalence is proved.

Now, we have that $f\in (K^2_{\theta })_{\bar \beta }^{G}$ if and only if $f\in \ker A_G^{\theta }$ , $\bar \beta f\in {K^2_{\theta }}$ , so $Gf=h_-+\theta h_+$ with $h_-\in H^2_-$ , $h_+\in H^2$ , and $h_+=P^+(\bar \theta Gf)$ . Assume (3). Then $A_G^{\theta }(\bar \beta f)\in ({K^2_{\theta }})_{\beta }$ if and only if $\beta A_G^{\theta }(\bar \beta f)\in {K^2_{\theta }}$ , i.e., $\theta P^+\bar \theta (\beta A_G^{\theta }(\bar \beta f))=0$ , so

$$ \begin{align*}0=&P^+\bar\theta \beta P_{\theta} G \bar\beta f=P^+\bar\theta \beta P_{\theta}\bar\beta(\theta h_+)=P^+\bar\theta \beta P_{\theta}\theta P^-\bar\beta h_+\\=&P^+\bar\theta \beta (I-\theta P^+\bar\theta)\theta P^-\bar\beta h_+=\beta P^-\bar\beta h_+-P^+\beta P^+(P^-\bar\beta h_+)\\=&P_{\beta} h_+=P_{\beta} P^+(\bar \theta Gf)=P_{\beta} (\bar \theta Gf).\end{align*} $$

Thus, (4) holds and $(4)\Rightarrow (3)$ is also clear.

Applying Theorem 5.6 to $\ker A_G^{\theta }$ for $X=\beta $ , we obtain the following.

Theorem 7.5 Let $\theta ,\beta $ be nonconstant inner functions, and let $G\in L^{\infty }$ . Then

(7.9) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_{\beta}\oplus M_G^{\prime}(\beta)\oplus M_G^{\prime\prime}(\beta),\end{align} $$

where, for $H=K^2_{\theta }$ ,

(7.10) $$ \begin{align} M_G^{\prime}(\beta):=M_{A_G^{\theta}}^{\prime}(M_{\beta})=P_{(K^2_{\theta})_{\beta}^{G}}(\bar\beta A_{\bar G}^{\theta}({K^2_{\theta}})_{\bar\beta}^{\bot})=P_{(K^2_{\theta})_{\beta}^{G}}(\bar \beta A_{\bar G}^{\theta} P_{\theta}(K^2_{\beta})),\end{align} $$

(7.11) $$ \begin{align} M_G^{\prime\prime}(\beta):=M_{A_G^{\theta}}^{\prime\prime}(M_{\beta})=P_{\ker A_G^{\theta}}({K^2_{\theta}})_{\bar\beta}^{\bot}=P_{\ker A_G^{\theta}}({\theta\bar\beta K^2_{\beta}}), \end{align} $$

abbreviating $(K^2_{\theta })_{\beta }^{\perp }={K^2_{\theta }}\ominus ({K^2_{\theta }})_{\beta }$ and $(K^2_{\theta })_{\bar \beta }^{\perp }={K^2_{\theta }}\ominus ({K^2_{\theta }})_{\bar \beta }$ , respectively.

Remark 7.6 Note that $M_G^{\prime }(\beta )$ , $M_G^{\prime \prime }(\beta )$ cannot be zero simultaneously, because then $\ker A_G^{\theta }$ would be $ \beta $ -invariant and thus $ \beta \ker A_G^{\theta }\subset \ker A_G^{\theta }$ . Repeating the reasoning we would get $\beta ^N\ker A_G^{\theta }\subset \ker A_G^{\theta }\subset K^2_{\theta }$ for any N. Thus $\bar \theta \beta ^N \ker A_G^{\theta }\subset \bar z \overline {H^2}$ and therefore $\bar \theta \ker A_G^{\theta }\subset \bar \beta ^N\bar z \overline {H^2}$ for all N, meaning that $ \ker A_G^{\theta }\subset \theta \bigcap _{N=1}^{\infty }\bar \beta ^N\bar z \overline {H^2}=\{0\}$ .

Now we study the relations between the decompositions of Theorems 7.1 and 7.5, and the usual conjugation on $K^2_{\theta }$ , defined by $C_{\theta } f=\theta \bar z\bar f$ . Note that, from Proposition 6.7, we have

(7.12) $$ \begin{align} C_{\theta}({K^2_{\theta}})_{\beta}=({K^2_{\theta}})_{\bar\beta}. \end{align} $$

Truncated Toeplitz operators are complex-symmetric for the conjugation $C_{\theta }$ , i.e.,

(7.13) $$ \begin{align} C_{\theta} {A_G^{\theta}}C_{\theta}=A_{\bar G}^{\theta}. \end{align} $$

Proposition 7.7 Let $G\in L^{\infty }$ , and let $\beta $ be an inner function. Then:

1. (1) $C_{\theta }(\ker A_G^{\theta })=\ker (A_G^{\theta })^*= \ker A_{\bar G}^{\theta }$ .

2. (2) $C_{\theta }(\ker A_G^{\theta })_{\bar \beta }=(\ker A_{\bar G}^{\theta })_{\beta }$ .

3. (3) $\,C_{\theta } P_{\ker A_G^{\theta }}C_{\theta }=P_{\ker A_{\bar G}^{\theta }}$ .

4. (4) $C_{\theta }(K^2_{\theta })_{\bar \beta }^{G}=(K^2_{\theta })_{\beta }^{\bar G}$ .

5. (5) $\,C_{\theta } P_{(K^2_{\theta })_{\bar \beta }^{G}}C_{\theta }=P_{(K^2_{\theta })_{\beta }^{\bar G}}$ .

Proof (1) was proved in [9, Section 3]. For (2), let $f\in (\ker A_G^{\theta })_{\bar \beta }$ . Then, by (7.13), $C_{\theta } f\in A_{\bar G}^{\theta }$ and $\beta C_{\theta } f=\beta \theta \bar z \bar f=\theta \bar z \overline {(\overline \beta f)}=C_{\theta } (\bar \beta f)\in \ker A_{\bar G}^{\theta }$ , by (1), because $\bar \beta f\in \ker A_G^{\theta }$ . Therefore (2) holds. Condition (3) follows from (2) and the properties of a conjugation. Equalities (4) and (5) follow from (1)–(3) and Proposition 5.12 taking into account that $(K^2_{\theta })_{\bar \beta }^{G}=\ker A_G^{\theta }\cap ({K^2_{\theta }})_{\bar \beta }$ and $(K^2_{\theta })_{\beta }^{\bar G}=\ker A_{\bar G}^{\theta }\cap ({K^2_{\theta }})_{ \beta }$ .

Note that, from Proposition 7.7, we have that $C_{\theta }(\ker A_{\bar G}^{\theta })_{\bar \beta }=(\ker A_{ G}^{\theta })_{\beta }$ . Therefore, we have the following.

Corollary 7.8 The orthogonal decomposition of $\ker A_G^{\theta }$ in Theorem 7.5 and the orthogonal decomposition of $\ker A_{\bar G}^{\theta }$ according to Theorem 7.1 are mapped into each other by the conjugation $C_{\theta }$ and we have $(\ker A_{ G}^{\theta })_{\beta }=C_{\theta }(\ker A_{\bar G}^{\theta })_{\bar \beta },\,\,M^{\prime }_G (\beta )=C_{\theta } M^{\prime }_{\bar G} (\bar \beta ),\,\,M^{\prime \prime }_G (\beta )=C_{\theta },M^{\prime \prime }_{\bar G} (\bar \beta ). $

Now we consider, in particular, the case $\beta =z$ and $X=M_{\bar z}$ (or simply $X=\bar z$ ), which allows us also to compare the results thus obtained with some other existing results on near $S^*$ -invariance for kernels of truncated Toeplitz operators.

The equalities (7.1) and (7.2) now take the form

(7.14) $$ \begin{align} &({K^2_{\theta}})_z=\ker T_{z \bar\theta}, \kern105pt ({K^2_{\theta}})_z^{\bot}=[\tilde k_0^{\theta}],\end{align} $$

(7.15) $$ \begin{align} &({K^2_{\theta}})_{\bar z}=z\ker T_{z \bar\theta}=\{\varphi\in K^2_{\theta} :\varphi (0)=0\}, \quad (K^2_{\theta})_{\bar z}^{\bot}=[k_0^{\theta}], \end{align} $$

where $[f]=\mathrm{span} \{f\}$ and we abbreviate $[(K^2_{\theta })_{\alpha }]_{K^2_{\theta }}^{\bot }$ to $(K^2_{\theta })_{\alpha }^{\bot }$ .

In what follows, we take $G\in L^{\infty }$ .

Proposition 7.9 Let $\theta $ be an inner function, and let $G\in L^{\infty }$ . We have that

(7.16) $$ \begin{align} (\ker A_G^{\theta})_z=\{\varphi\in (K^2_{\theta})_z:(P^+(\bar G \bar\theta C_{\theta} \varphi))\,(0)=0\}, \end{align} $$

(7.17) $$ \begin{align} (\ker A_G^{\theta})_{\bar z}&=\{\varphi\in (K^2_{\theta})_{\bar z}:(P^+( G \bar\theta \varphi))\,(0)=0\} \end{align} $$

(7.18) $$ \begin{align} &=\{\varphi\in K^2_{\theta}:\varphi (0)=0\,,\,(P^+( G \bar\theta \varphi))\,(0)=0\}. \end{align} $$

Proof Let $\varphi \in (K^2_{\theta })_z$ . We have $\varphi \in \ker A_G^{\theta }$ if and only if

(7.19) $$ \begin{align} G\varphi=\varphi_- + \theta\varphi_+,\,\,\,\varphi_{\pm} \in H^2_{\pm}, \end{align} $$

and $z\varphi \in \ker A_G^{\theta }$ if and only if

(7.20) $$ \begin{align} Gz\varphi=\psi_- + \theta\psi_+,\,\,\,\psi_{\pm} \in H^2_{\pm}. \end{align} $$

From (7.19), we also get

(7.21) $$ \begin{align} Gz\varphi=z\varphi_- + \theta z\varphi_+,\,\,\,\varphi_{\pm} \in H^2_{\pm}, \end{align} $$

and, if $\varphi _-=\bar z \overline {\eta _+}$ with $\eta _+\in H^2_+$ , we can write

(7.22) $$ \begin{align} Gz\varphi=\overline{\eta_+} + \theta z\varphi_+=\overline{\eta_+-\eta_+(0)}+\eta_+(0)+\theta z \varphi_+. \end{align} $$

Comparing (7.22) with (7.20), we conclude that $\varphi \in (\ker A_G^{\theta })_z$ if and only if $\eta _+(0)=0$ . Since $\varphi _-=P^-(G\varphi )$ , we have

$$\begin{align*}\eta_+=\bar z\overline{\varphi_-}=\bar z\overline{P^-(G\varphi)}=\bar z(zP^+(\bar z\bar G\bar\varphi))=P^+(\bar G\bar\theta C_{\theta}\varphi), \end{align*}$$

and thus (7.16) follows.

Now let $\varphi \in \ker A_G^{\theta }, \,\bar z\varphi \in \ker A_G^{\theta }$ , which is equivalent to

(7.23) $$ \begin{align} G\varphi=\varphi_- + \theta\varphi_+,\,\,\varphi(0)=0,\,\,G\bar z\varphi=\psi_- + \theta\psi_+, \end{align} $$

with $\varphi _{\pm } \in H^2_{\pm },\,\psi _{\pm } \in H^2_{\pm }.$ From the first equality in (7.23), we get

(7.24) $$ \begin{align} G\bar z\varphi=\bar z\varphi_- + \theta\bar z\varphi_+ =\bar z\varphi_- + \theta\bar z(\varphi_+-\varphi_+(0))+\varphi_+(0)\bar z(\theta-\theta(0)) +\varphi_+(0)\bar z \theta(0) \end{align} $$

and comparing with the third equality in (7.23) we conclude that (7.23) holds if and only if $\varphi (0)=0,\,\varphi _+(0)=0$ . Since $\varphi _+=P^+(\bar \theta G\varphi )$ , (7.17) holds.

Now, from Corollary 7.3, we have the following.

Proposition 7.10 Let $\theta $ be an inner function, and let $G\in L^{\infty }$ . The following are equivalent:

1. (1) $\ker A_G^{\theta }$ is ${K^2_{\theta }}$ -stable for $M_{\bar z}$ .

2. (2) $\ker A_G^{\theta } \bot k_0^{\theta }$ .

3. (3) $f(0)=0$ for all $f\in \ker A_G^{\theta }$ .

4. (4) $\ker A_G^{\theta }=(\ker A_G^{\theta })_{\bar z}\oplus [P_{\ker A_G^{\theta }}(zP_{\theta }\bar G\tilde k_0^{\theta })].$

If any of these conditions holds, then $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant (w.r.t. $H^2$ , w.r.t. ${K^2_{\theta }}$ ) with defect $1$ and almost-invariant with defect $1$ for $S_{\theta }^*=P_{\theta }\bar z {P_{\theta }}_{|K^2_{\theta }}$ .

Proof We have that $\ker A_G^{\theta }\,\bot \, k_0^{\theta }$ if and only if $ \ker A_G^{\theta }\,\bot \,1$ which is the same as $f(0)=0, \ \mathrm {for \ all}\,f\in \ker A_G^{\theta }$ . That is equivalent to $ \ker A_G^{\theta }\subset zK^2_{\theta }\cap K^2_{\theta }=z\ker T_{z\bar \theta }$ so (2) and (3) are equivalent and, by Corollary 7.3, they are also equivalent to (1) and to

$$\begin{align*}\ker A_G^{\theta}=(\ker A_G^{\theta})_{\bar z}\oplus [P_{\ker A_G^{\theta}}(zA_{\bar G}^{\theta} P^+(\theta\bar z))] \end{align*}$$

which in its turn is equivalent to (4). Since, with the notation of Theorem 7.1, $M^{\prime \prime }_G (\bar z)=\{0\}$ (so $M^{\prime }_G (\bar z)\ne \{0\}$ ), we have that $\ker A_G^{\theta }$ is $K^2_{\theta }$ -stable for $M_{\bar z}$ and nearly $S^*$ -invariant with defect $1$ .

From Corollary 7.4, we also get the following.

Proposition 7.11 Let $\theta $ be an inner function, and let $G\in L^{\infty }$ . The following are equivalent:

1. (1) $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant (w.r.t. $H^2$ , w.r.t. ${K^2_{\theta }}$ ).

2. (2) $A_G^{\theta }(\bar zf)\bot \tilde k_0^{\theta }$ , for all $f\in \ker {A_G^{\theta }}\,,\,f(0)=0$ .

3. (3) $P^+(G\bar \theta f)(0)=0$ , for all $f\in \ker {A_G^{\theta }}\,,\,f(0)=0$ .

4. (4) There exists $f_1\in \ker A_G^{\theta }$ , such that $f_1(0)\neq 0$ .

Proof We first remark that $(K^2_{\theta })^G_{\bar z}=\ker A_G^{\theta }\cap (K^2_{\theta })_{\bar z}=\{\varphi \in \ker A_G^{\theta }:\varphi (0)=0\}$ . To see $(1)\Leftrightarrow (2)$ recall from Corollary 7.4 that $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant if and only if $M_G^{\prime }(\bar z)=\{0\}$ , i.e., $A_G^{\theta }(\bar zf)\in \ker T_{z \bar \theta }= ({K^2_{\theta }})_z$ , for all $f\in \ker A_G^{\theta }\,,\,f(0)=0$ , which is equivalent to (2) since $(K^2_{\theta })^{\bot }_z =[\tilde k_0^{\theta }]$ . On the other hand, by Corollary 7.4, (1) is equivalent to

(7.25) $$ \begin{align} P_z(\bar\theta Gf)=0\,,\,{\mathrm for\,\, all }\ f\in\ker A_G^{\theta},\,f(0)=0. \end{align} $$

Since $f\in \ker A_G^{\theta }$ if and only if $Gf=f_-+\theta f_+$ with $f_{\pm }\in H^2_{\pm }$ , we have that for all $f\in \ker A_G^{\theta }\,,\,f(0)=0$ the condition (7.25) is equivalent to

$$\begin{align*}zP-{\bar z} {P^+}(\bar\theta f_-+f_+)=zP^-\bar zf_+=0. \end{align*}$$

This is equivalent to

$$\begin{align*}\bar z f_+\in H^2, \end{align*}$$

which holds if and only if

$$\begin{align*}f_+(0)=0. \end{align*}$$

In other words,

$$\begin{align*}P^+(\bar\theta Gf)\,(0)=0 \,\,{\mathrm for\,\, all}\ f\in\ker A_G^{\theta}\,,\,f(0)=0 .\end{align*}$$

So $(1)\Leftrightarrow (3)$ . Regarding the last equivalence, $(3)\Leftrightarrow (4)$ , we have that if $M_G^{\prime }(\bar z)=\{0\}$ , then $M_G^{\prime \prime }(\bar z)\neq \{0\}$ , so by (3) in Proposition 7.10, there must be some $f_1\in \ker A_G^{\theta }$ with $f_1(0)\neq 0$ . Conversely, assume that there exists $f_1\in \ker A_G^{\theta }$ with $f_1(0)\neq 0$ . Let g be any element of $\ker A_G^{\theta }$ . Then there exists $h_+\in H^2$ and $g_{-},h_-\in H^2_-$ such that $\bar \theta g=g_-$ and $G\,g=h_-+\theta h_+$ , i.e.,

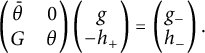$$ \begin{align*} \begin{pmatrix} \bar\theta & 0 \\ G & \theta \end{pmatrix} \begin{pmatrix} g \\ -h_+ \end{pmatrix}= \begin{pmatrix} g_{-} \\ h_- \end{pmatrix}. \end{align*} $$

Analogous relation holds also for $f_1$ , so

$$ \begin{align*} \begin{pmatrix} \bar\theta & 0 \\ G & \theta \end{pmatrix} \begin{pmatrix} g & f_ 1\\ -h_+ & f_2 \end{pmatrix}= \begin{pmatrix} g_{-} & f_{1-} \\ h_- & f_{2-} \end{pmatrix} \end{align*} $$

with $f_2\in H^2$ , $f_{1-},f_{2-}\in H^2_{-}$ . Calculating the determinants on both sides, we get

$$ \begin{align*} gf_2+h_+f_1=g_{-}f_{2-}-h_-f_{1-}. \end{align*} $$

Note that the left-hand side is an element of $H^1$ and the right-hand side is an element of $\overline {zH^1}$ . Thus, both have to be $0$ and it follows that $h_+=\frac {gf_2}{f_1}$ , with $f_1(0)\neq 0$ , so $h_+$ must vanish at $0,$ whenever $g(0)=0$ , i.e., for all $g=H_{\bar z}^{A_G^{\theta }}$ . So (3) follows.

As a consequence of Propositions 7.9 and 7.10 and Theorem 7.1, we can now state the following.

Theorem 7.12 Let $\theta $ be an inner function and $G\in L^{\infty }$ . We have that either:

1. (1) there exists $f_1 \in \ker A_G^{\theta }$ with $f_1(0)\ne 0$ and, in that case, $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant (w.r.t. $H^2$ , w.r.t. ${K^2_{\theta }}$ ) and

   (7.26) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_{\bar z}\oplus [P_{\ker A_G^{\theta}}k_0^{\theta}]=(\ker A_G^{\theta})_{\bar z}\oplus [P_{\ker A_G^{\theta}}1] \,, \end{align} $$

   or

2. (2) $f(0)=0$ for all $f\in \ker A_G^{\theta }$ and, in that case, $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant with defect $1$ and ${K^2_{\theta }}$ -stable for $M_{\bar z}$ , and we have

   (7.27) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_{\bar z}\oplus [P_{\ker A_G^{\theta}}(zA_{\bar G}^{\theta}\tilde k_0^{\theta})]=({K^2_{\theta}})_{\bar z}^G. \end{align} $$

Remark 7.13 We recover in Theorem 7.12 some results obtained, in a different way, in [27, Section 4], namely that $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant (w.r.t. ${K^2_{\theta }}$ ) if there exists $f_1\in \ker A_G^{\theta }$ with $f_1(0)\neq 0$ , and $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant with defect $1$ if $f(0)=0$ for all $f\in \ker A_G^{\theta }$ . Another interesting result from [27] is that, in the latter case, if n is the greatest natural number such that $\ker A_G^{\theta }\subset z^nH^2$ , then $z^{-n}\,{\ker A_G^{\theta }}$ is a nearly $S^*$ -invariant subspace. Again, we can obtain this result differently, by observing that

(7.28) $$ \begin{align} z^{-n}\,{\ker A_G^{\theta}}=\ker A_{Gz^n,} \end{align} $$

where not all functions in $\ker A_{Gz^n}$ vanish at $0$ , so by Proposition 7.10, it is nearly $\bar z$ -invariant (w.r.t. ${K^2_{\theta }}$ ). To prove (7.28), take $f\in \ker A_G^{\theta }\subset {K^2_{\theta }}\cap z^n H^2$ , then for some $h_+\in H^2$ , $h_-\in H^2_-$ , we have $Gf=h_-+\theta h_+$ . Thus $(Gz^n)(z^{-n}f)=h_-+\theta h_+$ , so $f=z^n (z^{-n}f)$ with $z^{-n}f \in \ker A_{Gz^n}^{\theta }$ . For the reverse inclusion, note that, if $ (Gz^n)f=h_-+\theta h_+$ , then $G(z^nf)=h_-+\theta h_+$ and $z^nf\in \ker A_G^{\theta }$ , so $z^n \ker A_{Gz^n}^{\theta }\subset \ker A_G^{\theta }$ .

We now compare the decomposition obtained in Example 5.2 with (7.26). We can assume that $G\in {K^2_{\theta }}$ , and $\ker A_G^{\theta }=\gamma {K^2_{\beta }}$ with $\beta <\theta $ , $\gamma =\theta /\beta $ , $\gamma (0)=0$ , $\beta <G^i$ (inner part of G). So, by Theorem 7.12, $\ker A_G^{\theta }$ is nearly $\bar z$ -invariant with defect $1$ and ${K^2_{\theta }}$ -invariant for $M_{\bar z}$ , and we have

$$ \begin{align*} \ker A_G^{\theta}=(\ker A_G^{\theta})_{\bar z} \oplus [P_{\ker A_G^{\theta}}(zA_{\bar G}^{\theta} \tilde k_0^{\theta})], \end{align*} $$

where $P_{\ker A_G^{\theta }}=P_{\gamma {K^2_{\beta }}}=\gamma P_{\beta } \bar \gamma P^+$ . One can see that

$$ \begin{align*} (\ker A_G^{\theta})_{\bar z}=(\gamma {K^2_{\beta}})_{\bar z}=\gamma({K^2_{\beta}})_{\bar z}.\ \end{align*} $$

It is left to show that $[P_{\ker A_G^{\theta }}(zA_{\bar G}^{\theta } \tilde k_0^{\theta })]=[\gamma k_0^{\beta }]$ . Indeed, we have

(7.29) $$ \begin{align} P_{\gamma {K^2_{\beta}}}(zA_{\bar G}^{\theta} \tilde k_0^{\theta})=\gamma P_{\beta} \bar\gamma (zA_{\bar G}^{\theta} \tilde k_0^{\theta})=\gamma P_{\beta} \bar\gamma\theta\bar G, \end{align} $$

because

$$ \begin{align*} A_{\bar G}^{\theta} \tilde k_0^{\theta}=P_{\theta}(\bar G\bar z(\theta-\theta(0)))=P_{\theta}(\bar G\bar z\theta)-P_{\theta}(\bar G\bar z\theta(0))=C_{\theta} G=\theta\bar z\bar G. \end{align*} $$

Hence, from (7.29),

$$ \begin{align*} P_{\gamma {K^2_{\beta}}}(zA_{\bar G}^{\theta} \tilde k_0^{\theta})=\gamma P_{\beta} (\bar\gamma \theta \bar G)=\gamma P_{\beta} (\beta\bar G), \end{align*} $$

where $\beta \bar G\in \overline {H^2}$ , because $\beta $ divides the inner factor $G^i$ . Thus $P_{\beta }(\beta \bar G)=c\in \mathbb {C}$ and $\gamma P_{\beta }(\beta \bar G)=c\gamma k_0^{\beta }$ .

Note that the dichotomy of Theorem 7.12 does not extend to other cases with $\beta \neq z$ , as we show in the following simple example where both $M_G^{\prime }(\bar \beta )$ and $M_G^{\prime \prime }(\bar \beta )$ are different from $\{0\}$ .

Example 7.14 Let $G=z^3$ , $\theta =z^4$ . Then $\ker A_G^{\theta }=zK^2_{z^3}$ so, for $X=\bar z^2$ , the decomposition (7.6) has the form

$$ \begin{align*} \ker A_G^{\theta}= (\ker A_G^{\theta})_{\bar z^2}\oplus M_G^{\prime}(\bar z^2) \oplus M_G^{\prime\prime}(\bar z^2)= [z^3] \oplus [z^2] \oplus [z]. \end{align*} $$

One can also study the z-invariance properties of kernels of truncated Toeplitz operators and obtain the decomposition given in Theorem 7.5 with $\beta =z$ , using Theorem 7.12 and Corollary 7.8.

Theorem 7.15 Let $\theta $ be an inner function and $G\in L^{\infty }$ . We have either

(7.30) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_z\oplus [P_{\ker A_G^{\theta}}\tilde k_0^{\theta}], \end{align} $$

where the second term in the orthogonal sum corresponds to $ M_G^{\prime \prime }(\bar z)$ in Theorem 7.1, or

(7.31) $$ \begin{align} \ker A_G^{\theta}=(\ker A_G^{\theta})_z\oplus [P_{\ker A_G^{\theta}}(zA_{\bar G}^{\theta}k_0^{\theta})], \end{align} $$

where the second term in the orthogonal sum corresponds to $ M_G^{\prime }(z)$ in Theorem 7.1.

Corollary 7.16 The following are equivalent:

1. (1) $\ker A_G^{\theta }$ is nearly z-invariant (w.r.t. ${K^2_{\theta }}$ ).

2. (2) $\ker (A_{\bar G}^{\theta })$ is nearly $\bar z$ -invariant (w.r.t. ${K^2_{\theta }}$ ).

3. (3) $\langle \bar z A_{\bar G}^{\theta } k_0^{\theta }, f\rangle =0$ for all $f\in \ker A_G^{\theta }$ , $(C_{\theta } f)(0)=0$ .

4. (4) $(P^-Gf)\in \bar z H_-^2$ for all $f\in \ker A_G^{\theta }$ , $(C_{\theta } f)(0)=0$ .

Proof The equivalence between (1) and (2) is a direct consequence of the previous results.

By Theorem 7.11, (2) is equivalent to the fact that, for all $ f\in \ker A_G^{\theta }$ such that $ f(0)=0$ , the first equality holds and

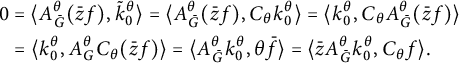$$ \begin{align*} \begin{aligned} 0&=\langle A_{\bar G}^{\theta}(\bar z f),\tilde k_0^{\theta}\rangle= \langle A_{\bar G}^{\theta}(\bar z f),C_{\theta} k_0^{\theta}\rangle =\langle k_0^{\theta},C_{\theta} A_{\bar G}^{\theta}(\bar z f)\rangle\\&= \langle k_0^{\theta},A_G^{\theta} C_{\theta} (\bar z f)\rangle =\langle A_{\bar G}^{\theta}k_0^{\theta},\theta\bar f\rangle = \langle \bar z A_{\bar G}^{\theta}k_0^{\theta},C_{\theta} f \rangle. \end{aligned} \end{align*} $$

For $\tilde f=C_{\theta } f$ , we have, thus, that the above is equivalent to $\langle \bar z A_{\bar G}^{\theta }, \tilde f\rangle =0$ for all $\tilde f\in \ker A_G^{\theta }$ , $(C_{\theta } \tilde f)(0)=0$ . Hence (2) $\Leftrightarrow $ (3).

Now we show that (3) $\Leftrightarrow $ (4). Note that, for $ f$ such as in (3), we have

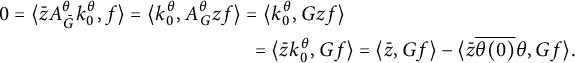$$ \begin{align*} 0=\langle \bar z A_{\bar G}^{\theta}k_0^{\theta}, f \rangle &= \langle k_0^{\theta}, A_G^{\theta} z f \rangle = \langle k_0^{\theta}, Gz f \rangle \\ &\qquad\qquad\qquad = \langle \bar z k_0^{\theta}, G f \rangle = \langle \bar z, G f \rangle - \langle \bar z \overline{\theta(0)}\theta, G f \rangle. \end{align*} $$

Since $ f\in \ker A_G^{\theta }$ , we have that $G f=P^-(G f)+\theta P^+\bar \theta (G f)$ , so the previous equality is equivalent to

$$ \begin{align*} \begin{aligned} 0=&\langle \bar z, P^-G f\rangle - \overline{\theta(0)} \langle \bar z \theta, P^-G f\rangle-\overline{\theta(0)}\langle \bar z \theta, \theta P^+\bar\theta G f\rangle \\ =& \langle \bar z, P^-G f\rangle - \overline{\theta(0)} \langle P^-\bar z \theta, P^-G f\rangle\\ =& \langle \bar z, P^-G f\rangle - \overline{\theta(0)}\theta(0) \langle \bar z, P^-G f\rangle\\=&(1- |{\theta(0)}|^2)\langle \bar z, P^-G f\rangle. \end{aligned} \end{align*} $$

This is equivalent to

$$ \begin{align*}\langle \bar z, P^-Gf\rangle=0,\end{align*} $$

i.e., $P^-G f\in \bar z H_-^2.$

Analogously, we have the following.

Corollary 7.17 The following are equivalent:

1. (1) $\ker A_G^{\theta }$ is nearly z-invariant with defect $1$ (w.r.t. ${K^2_{\theta }}$ ).

2. (2) $\ker (A_G^{\theta })^*$ is nearly $\bar z$ -invariant with defect $1$ (w.r.t. ${K^2_{\theta }}$ ).

3. (3) $\ker A_G^{\theta }\bot \tilde k_0^{\theta }$ .

4. (4) $(C_{\theta } f)(0)=0$ for all $f\in \ker A_G^{\theta }$ .

5. (5) $z\ker A_G^{\theta } \subset {K^2_{\theta }}$ .