Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T04:39:10.248Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalization of Epstein Zeta Functions

Published online by Cambridge University Press:  20 November 2018

S. Minakshisundaram
S. Minakshisundaram*
Affiliation:
Institute for Advanced Study
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§ 1. An Epstein zeta function (in its simplest form) is a function represented by the Dirichlet's series 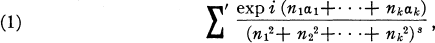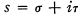where a1… ak are real and n1, n2, … nk run through integral values. The properties of this function are well known and the simplest of them were proved by Epstein [2, 3]. The aim of this note is to define a general class of Dirichlet's series, of which the above can be viewed as an instance, and to discuss the problem of analytic continuation of such series.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 1 , Issue 4 , 01 August 1949 , pp. 320 - 327
Copyright
Copyright © Canadian Mathematical Society 1949

References

1 Each eigenvalue being repeated according to its multiplicity and the eigenfunctions being real.

2 Though the Green's functions are different in the two boundary problems we use the same notation G(x, y; t) and there need be no confusion.

3 The iterated Green's function of Δu will belong to L2 for a sufficiently high order of iteration, from which it will follow that

is convergent if a is large and

will be absolutely convergent for large σ.

4 This series for the two dimensional domain was first studied by T. Carleman [1].

5 The author is indebted to Professor H. Weyl for this remark.

6 For a detailed discussion of these inequalities and the determination of the Green's function of the heat equation by Neumann's series cf. E. E. Levi [4, pp. 261-262.] We derive the inequality (21) assuming cos(rn) = 0(r) for small r. Similar inequalities can also be derived with cos (rn) = 0(ra) 0 < a ≤ 1 which is a regularity condition on B.