Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koekoek, Roelof
1992.
Generalizations of a q-analogue of Laguerre polynomials.
Journal of Approximation Theory,
Vol. 69,
Issue. 1,
p.
55.
Alvarez-Nodarse, R.
and
Marcellán, F.
1998.
On the modifications of classical orthogonal polynomials: The symmetric case.
Approximation Theory and its Applications,
Vol. 14,
Issue. 1,
p.
8.
Álvarez-Nodarse, R.
and
Petronilho, J.
2004.
On the Krall-type discrete polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 295,
Issue. 1,
p.
55.
Diekema, Enno
and
Koornwinder, Tom H.
2012.
Generalizations of an integral for Legendre polynomials by Persson and Strang.
Journal of Mathematical Analysis and Applications,
Vol. 388,
Issue. 1,
p.
125.
Cao, Jian
2013.
Some Integrals Involvingq-Laguerre Polynomials and Applications.
Abstract and Applied Analysis,
Vol. 2013,
Issue. ,
p.
1.
Essadiq, A.
Ghanmi, A.
and
Intissar, A.
2016.
A q-analogue of the weighted Bergman space on the disk and associated second q-Bargmann transform.
Journal of Mathematical Analysis and Applications,
Vol. 443,
Issue. 2,
p.
1311.
Niu, Da-Wei
and
Li, Long
2018.
q-Laguerre polynomials and related q-partial differential equations.
Journal of Difference Equations and Applications,
Vol. 24,
Issue. 3,
p.
375.
Filipuk, Galina
Mañas-Mañas, Juan F.
and
Moreno-Balcázar, Juan J.
2022.
Second-order difference equation for Sobolev-type orthogonal polynomials: Part I: theoretical results.
Journal of Difference Equations and Applications,
Vol. 28,
Issue. 7,
p.
971.
Cao, Jian
Srivastava, H. M.
and
Zhang, Yue
2025.
Quantum (or q‐) operator equations and associated partial differential equations for bivariate Laguerre polynomials with applications to the q‐Hille‐Hardy type formulas.
Mathematical Methods in the Applied Sciences,
Vol. 48,
Issue. 1,
p.
308.


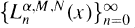 which are generalizations of the classical (generalized) Laguerre polynomials
which are generalizations of the classical (generalized) Laguerre polynomials 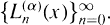 These polynomials were shown to be orthogonal on the interval [0, ∞) with respect to the inner product
These polynomials were shown to be orthogonal on the interval [0, ∞) with respect to the inner product