Published online by Cambridge University Press: 20 November 2018
Suppose throughout that {kn} is a sequence of positive integers, that

that k0 = 1 if l0 = 1, and that {un(r)}; (r = 0, 1, …, kn – 1, n = 0, 1, …) is a sequence of real numbers. We shall be concerned with the problem of establishing necessary and sufficient conditions for there to be a function a satisfying
(1)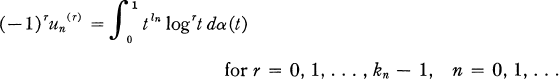
and certain additional conditions. The case l0 = 0, kn = 1 for n = 0, 1, … of the problem is the version of the classical moment problem considered originally by Hausdorff [5], [6], [7]; the above formulation will emerge as a natural generalization thereof.