Published online by Cambridge University Press: 20 November 2018
1. Introduction. The averaging operator 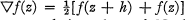 has an extensive literature, the most detailed account being that of Nörlund
has an extensive literature, the most detailed account being that of Nörlund
(4). In discussing solutions of the functional relation
1.1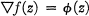
he defines a “principal solution” (4, p. 41) by means of a summability process, and later, working in terms of complex numbers, he obtains (4, p. 70) a principal solution of (1.1) by means of a contour integral. He distinguishes his principal solution from other solutions, by showing that it is continuous at h = 0.