Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T02:41:24.083Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Euler Number Sequences: Asymptotic Estimates and Congruences

Published online by Cambridge University Press:  20 November 2018

D. J. Leeming  and
R. A. Macleod
D. J. Leeming
Affiliation:
University of Victoria, Victoria, British Columbia
R. A. Macleod
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define (as in [7]) integer sequences 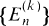one for each positive integer k ≧ 2, by

1.1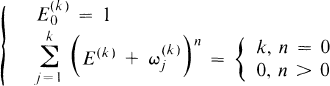

where 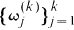are the kth roots of unity and (E(k))n is replaced by 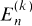after multiplying out. We note that (1.1) implies 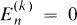, n ≠ 0 (mod k).

In [7], we considered some special properties of these number sequences, proved several congruences and conjectured several others. This paper is a continuation of the work presented in [7].

In Section 2 we demonstrate the asymptotic rate of growth of the numbers 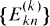by showing that

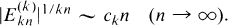
In Section 3 we present a large number of congruences (modulo 2048), some of which are proved or can be proved by the techniques presented herein, and other congruences which appear to be true on the basis of numerical evidence.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 3 , 01 June 1983 , pp. 526 - 546
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Brun, V., Stubban, J. O., Fjeldstad, J. E., Lyche, R. Tarnbs, Aubert, K. E., Ljunggen, W. and Jacobsthal, E., On the divisibility of the difference between two binomial coefficients, Den 1 lte Skandinaviski Matematiker Kongress, Trondheim (1949), 42–54.Google Scholar
2. Carlitz, L., Some arithmetic properties of a special sequence of integers, Can. Math. Bull. 19 (1976), 425–429.Google Scholar
3. Fjeldstad, J. E., A proof of the formula . Norsk. Mat. Tidsskr. 24 (1942), 13–17. (Norwegian)Google Scholar
4. Jacobsthal, E., Number-theoretical properties of binomial coefficients, Norske Vid. Selsk. Skr., Trondhjem (1942), no. 4 (1945) (Norwegian-French summary).Google Scholar
5. Knuth, D., The art of computer programming, I (Addison-Wesley, Reading, Mass., 1973).Google Scholar
6. Leeming, D. J., An asymptotic estimate for the Bernoulli and Euler numbers, Can. Math. Bull. 20 (1977), 109–111.Google Scholar
7. Leeming, D. J. and MacLeod, R. A., Some properties of generalized Euler numbers, Can. J. Math. 33 (1981), 606–617.Google Scholar
8. Lucas, E., Théorie des nombres, Tome I, Librarie Scientifique et Technique Albert Blanchard, Paris (1961) 417–420, (cf. N.J. Fine, Amer. Math. Monthly 54 (1947), 589-592).Google Scholar
9. Jan, G.-Mikusinski, Sur les fonctions , Ann. Soc. Polon. Math. 21 (1948), 46–51.Google Scholar
10. Trench, W. F., On periodicities of certain sequences of residues, Amer. Math. Monthly 67 (1960), 652–656.Google Scholar
11. Zabek, S., Sur la periodicité modulo m des suites de nombres , Ann. Univ. Marie Curie-Sklodovska. Sect. A10 (1956), 37–47 (1958).Google Scholar