Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T16:09:53.058Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Triple Homomorphisms and Derivations

Published online by Cambridge University Press:  20 November 2018

Jorge J. Garcés  and
Antonio M. Peralta
Jorge J. Garcés
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain, e-mail: jgarces@ugr.es, aperalta@ugr.es
Antonio M. Peralta
Affiliation:
Departamento de Análisis Matemático, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain, e-mail: jgarces@ugr.es, aperalta@ugr.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce generalized triple homomorphisms between Jordan–Banach triple systems as a concept that extends the notion of generalized homomorphisms between Banach algebras given by K. Jarosz and B. E. Johnson in 1985 and 1987, respectively. We prove that every generalized triple homomorphism between 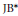$\text{J}{{\text{B}}^{*}}$-triples is automatically continuous. When particularized to 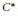${{C}^{*}}$-algebras, we rediscover one of the main theorems established by Johnson. We will also consider generalized triple derivations from a Jordan–Banach triple 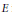$E$ into a Jordan–Banach triple 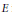$E$-module, proving that every generalized triple derivation from a 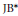$\text{J}{{\text{B}}^{*}}$-triple 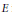$E$ into itself or into ${{E}^{*}}$is automatically continuous.

Keywords

46L0546L7047B4817C6546K7046L4047B4747B49generalized homomorphismgeneralized triple homomorphismgeneralized triple derivationBanach algebraJordan-Banach triplec*-algebraJB*-triple
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 783 - 807
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Akkar, M. and Laayouni, M., Théorèmes de factorisation dans les algèbres normées complètes non associatives. Colloq. Math. 70(1996), 253–264.Google Scholar
[2] Bade, W. G. and Curtis, P. C., Homomorphisms of commutative Banach algebras. Amer. J. Math. 82(1960), 589–608. http://dx.doi.org/10.2307/2372972 Google Scholar
[3] Barton, T. J., Dang, T., and Horn, G., Normal representations of Banach Jordan triple systems. Proc. Amer. Math. Soc. 102(1988), 551–555. http://dx.doi.org/10.1090/S0002-9939-1988-0928978-2 Google Scholar
[4] Becerra-Guerrero, J., Lopez, G., Peralta, A. M. and Rodríguez, A., Relatively weakly open sets in closed unit balls of Banach spaces and real JB*-triples of finite rank. Math. Ann. 330(2004), 45–58.Google Scholar
[5] Bunce, L. J., Chu, C.-H., and Zalar, B., Structure spaces and decomposition in JB*-triples. Math. Scand. 86(2000), 17–35.Google Scholar
[6] Burgos, M., Fernández-Polo, F. J., Garcés, J., Martínez, J., and Peralta, A. M., Orthogonality preservers in C*-algebras, JB*-algebras and JB*-triples. J. Math. Anal. Appl. 348(2008), 220–233. http://dx.doi.org/10.1016/j.jmaa.2008.07.020 Google Scholar
[7] Cleveland, S. B., Homomorphisms of non-commutative *-algebras. Pacific J. Math. 13(1963), 1097–1109.Google Scholar
[8] Cuntz, J., On the continuity of semi-norms on operator algebras. Math. Ann. 220(1976), 171–183. http://dx.doi.org/10.1007/BF01351703 Google Scholar
[9] Dales, H. G., Automatic continuity: a survey. Bull. London Math. Soc. 10(1978), 129–183. http://dx.doi.org/10.1112/blms/10.2.129 Google Scholar
[10] H. G. Dales, , Banach algebras and automatic continuity. London Math. Soc. Monogr. 24, Oxford University Press, New York, 2000.Google Scholar
[11] Dang, T. and Friedman, Y., Classification of JBW*-triple factors and applications. Math. Scand. 61(1987), 292–330.Google Scholar
[12] Edwards, C. M., Fernández-Polo, F. J., Hoskin, C. S., and Peralta, A. M., On the facial structure of the unit ball in a JB*-triple. J. Reine Angew. Math. 641(2010), 123–144.Google Scholar
[13] Fernandez-Polo, F. J., Garces, Jorge J., and Peralta, A. M., A Kaplansky Theorem for JB*-triples. Proc. Amer. Math. Soc., to appear. http://dx.doi.org/10.1090/S0002-9939-2012-11157-8 Google Scholar
[14] Fernández-Polo, F. J., Martánez Moreno, J., and Peralta, A. M., Surjective isometries between real JB*-triples. Math. Proc. Cambridge Philos. Soc. 137(2004), 709–723.Google Scholar
[15] Friedman, Y. and Russo, B., Structure of the predual of a JBW*-triple. J. Reine Angew. Math. 356(1985), 67–89.Google Scholar
[16] Hanche-Olsen, H. and Stormer, E., Jordan operator algebras. Monogr. Stud. Math. 21, Pitman, London–Boston–Melbourne, 1984.Google Scholar
[17] Isidro, J. M.,Kaup, W., and RodrÍguez, A., On real forms of JB*-triples. Manuscripta Math. 86(1995), 311–335. http://dx.doi.org/10.1007/BF02567997 Google Scholar
[18] Jarosz, K., Perturbations of Banach algebras. Lecture Notes in Math. 1120, Springer-Verlag, Berlin, 1985.Google Scholar
[19] Johnson, B. E., Continuity of homomorphisms of operator algebras II. J. London Math. Soc. (2) 1(1969), 81–84. http://dx.doi.org/10.1112/jlms/s2-1.1.81 Google Scholar
[20] Johnson, B. E., Continuity of generalized homomorphisms. Bull. London Math. Soc. 19(1987), 67–71. http://dx.doi.org/10.1112/blms/19.1.67 Google Scholar
[21] Johnson, B. E., Approximately multiplicative functional. J. London Math. Soc. (2) 37(1988), 294–316. http://dx.doi.org/10.1112/jlms/s2-37.2.294 Google Scholar
[22] Kaup, W., A Riemann Mapping Theorem for bounded symmetric domains in complex Banach spaces. Math. Z. 183(1983), 503–529. http://dx.doi.org/10.1007/BF01173928 Google Scholar
[23] Kaup, W., On real Cartan factors. Manuscripta Math. 92(1997), 191–222. http://dx.doi.org/10.1007/BF02678189 Google Scholar
[24] Loos, O., Bounded symmetric domains and Jordan pairs. Math. Lectures, University of California, Irvine, 1977.Google Scholar
[25] Peralta, A. M. and Russo, B., Automatic continuity of derivations on C*-algebras and JB*-triples. Preprint, 2010 Google Scholar
[26] Rickart, C., The uniqueness of norm problem in Banach algebras. Ann. of Math. 51(1950), 615–628. http://dx.doi.org/10.2307/1969371 Google Scholar
[27] A. M. Sinclair, , Homomorphisms from C*-algebras. Proc. London Math. Soc. (3) 29(1975), 435–452. http://dx.doi.org/10.1112/plms/s3-29.3.435 Google Scholar
[28] A. M. Sinclair, , Automatic continuity of linear operators. London Math. Soc. Lecture Notes 21, Cambridge University Press, Cambridge–New York–Melbourne, 1976.Google Scholar
[29] Yood, B., Homomorphisms on normed algebras.Pacific J. Math. 8(1958), 373–381.Google Scholar