Published online by Cambridge University Press: 20 November 2018
Many of the basic results of HP theory on the disk Δ = {|z| < 1} are proved using the Cauchy-Stieltjes representation
1.1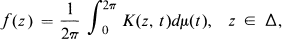
and the Poisson-Stieltjes representation
1.2
Here, μ:R → C is a complex-valued function of a real variable that is of bounded variation on [0, 2π] such that μ(t + 2π) = μ(t) + μ(2t) — μ(0), t ∊ R,

is the Cauchy kernel, and

is the Poisson kernel. It is therefore natural to generalize these representations in such a way that some of the basic properties and results carry over. Such a generalization occurs when the assumption that μ is of bounded variation on [0, 2μ] is replaced by the requirement that it is measurable and bounded on [0, 2μ] (cf. [9]). The integrals in (1.1) and (1.2) are then defined by a formal integration by parts. After some preliminaries in Section 2, we catalogue a variety of results which remain valid in Section 3.