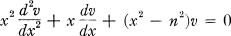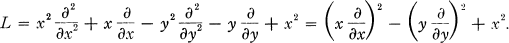Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1968.
Lie Theory and Special Functions.
Vol. 43,
Issue. ,
p.
330.
Miller, Jr., Willard
1970.
Lie Theory and q-Difference Equations.
SIAM Journal on Mathematical Analysis,
Vol. 1,
Issue. 2,
p.
171.
Miller, Jr., Willard
1970.
Lie Theory and Special Functions Satisfying Second Order Nonhomogeneous Differential Equations.
SIAM Journal on Mathematical Analysis,
Vol. 1,
Issue. 2,
p.
246.
Miller, Jr, Willard
1974.
Lie Theory and Separation of Variables. I: Parabolic Cylinder Coordinates.
SIAM Journal on Mathematical Analysis,
Vol. 5,
Issue. 4,
p.
626.
Miller, Willard
1975.
Theory and Application of Special Functions.
p.
305.
Mori, Masao
1978.
On Lie algebraic properties of the step operators acting on P or confluent P functions.
Journal of Mathematical Physics,
Vol. 19,
Issue. 5,
p.
1057.
Carroll, R.
and
Jones, D. S.
1984.
Transmutation via the momentum plane.
Mathematical Methods in the Applied Sciences,
Vol. 6,
Issue. 1,
p.
467.
1985.
Transmutation Theory and Applications.
Vol. 117,
Issue. ,
p.
323.
Durand, Loyal
2003.
Fractional operators and special functions. I. Bessel functions.
Journal of Mathematical Physics,
Vol. 44,
Issue. 5,
p.
2250.
Khan, Subuhi
and
Mittal, Archana
2006.
Representation of lie algebra T3 and generalized bessel functions.
Reports on Mathematical Physics,
Vol. 58,
Issue. 1,
p.
1.
Khan, Subuhi
and
Yasmin, Ghazala
2006.
Generalized Bessel Functions and Lie Algebra Representation.
Mathematical Physics, Analysis and Geometry,
Vol. 8,
Issue. 4,
p.
299.
Khan, Subuhi
Yasmin, Ghazala
and
Mittal, Archana
2007.
Representation of Lie algebra T3 and 2-variable 2-parameter Bessel functions.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
500.
Khan, Subuhi
and
Hassan, Nader Ali Makboul
2008.
Generating relations of Tricomi and Hermite–Tricomi functions using Lie algebra representation.
Applied Mathematics and Computation,
Vol. 202,
Issue. 1,
p.
86.
Khan, Subuhi
Khan, M.A.
and
Khan, Rehana
2008.
Lie-theoretic generating relations involving multi-variable bessel functions of two indices.
Reports on Mathematical Physics,
Vol. 62,
Issue. 2,
p.
183.
Khan, Subuhi
and
Khan, Rehana
2009.
Lie-theoretic generating relations involving multi-variable Hermite–Tricomi functions.
Integral Transforms and Special Functions,
Vol. 20,
Issue. 5,
p.
365.
Chirikjian, Gregory S.
2009.
Stochastic Models, Information Theory, and Lie Groups, Volume 1.
p.
31.
Makboul Hassan, Nader Ali
2014.
Generating relations of multi-variable Tricomi functions of two indices using Lie algebra representation.
Arab Journal of Mathematical Sciences,
Vol. 20,
Issue. 1,
p.
101.
Shehata, A.
2018.
Certain Generating Matrix Relations of Generalized Bessel Matrix Polynomials from the View Point of Lie Algebra Method.
Bulletin of the Iranian Mathematical Society,
Vol. 44,
Issue. 4,
p.
1025.
Shehata, Ayman
2019.
Certain Properties of Generalized Hermite-Type Matrix Polynomials Using Weisner’s Group Theoretic Techniques.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 50,
Issue. 2,
p.
419.
Yang, Xiao-Jun
2021.
An Introduction to Hypergeometric, Supertrigonometric, and Superhyperbolic Functions.
p.
345.