Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T04:44:59.740Z Has data issue: false hasContentIssue false
  • English
  • Français

The Genus of a Random Bipartite Graph

Part of: Low-dimensional topology Graph theory

Published online by Cambridge University Press:  29 August 2019

Yifan Jing  and
Bojan Mohar
Yifan Jing
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC, Canada Email: yifanjing17@gmail.commohar@sfu.ca
Bojan Mohar
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC, Canada Email: yifanjing17@gmail.commohar@sfu.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Archdeacon and Grable (1995) proved that the genus of the random graph 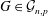$G\in {\mathcal{G}}_{n,p}$ is almost surely close to 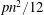$pn^{2}/12$ if 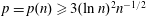$p=p(n)\geqslant 3(\ln n)^{2}n^{-1/2}$. In this paper we prove an analogous result for random bipartite graphs in 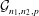${\mathcal{G}}_{n_{1},n_{2},p}$. If $n_{1}\geqslant n_{2}\gg 1$, phase transitions occur for every positive integer $i$ when 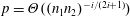$p=\unicode[STIX]{x1D6E9}((n_{1}n_{2})^{-i/(2i+1)})$. A different behaviour is exhibited when one of the bipartite parts has constant size, i.e., 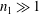$n_{1}\gg 1$ and 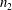$n_{2}$ is a constant. In that case, phase transitions occur when 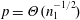$p=\unicode[STIX]{x1D6E9}(n_{1}^{-1/2})$ and when 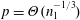$p=\unicode[STIX]{x1D6E9}(n_{1}^{-1/3})$.

Keywords

Genusgraph genustopological embeddingsurface embeddingrandom bipartite graph

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Secondary: 57M15: Relations with graph theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1607 - 1623
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

B.M. was supported in part by the NSERC Discovery Grant R611450 (Canada), by the Canada Research Chairs program, and by the Research Project J1-8130 of ARRS (Slovenia). On leave from IMFM & FMF, Department of Mathematics, University of Ljubljana.

References

Alon, N. and Spencer, J. H., The probabilistic method, Fourth ed., Wiley Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., Hoboken, NJ, 2016.Google Scholar
Archdeacon, D. and Grable, D. A., The genus of a random graph. Discrete Math. 142(1995), 1–3, 21–37. https://doi.org/10.1016/0012-365X(95)00215-ICrossRefGoogle Scholar
Bollobás, B., Random graphs, Second ed., Cambridge Studies in Advanced Mathematics, 73, Cambridge University Press, Cambridge, 2001. https://doi.org/10.1017/CBO9780511814068CrossRefGoogle Scholar
Diestel, R., Graph theory, Fourth ed., Graduate Texts in Mathematics, 173, Springer, Heidelberg, 2010. https://doi.org/10.1007/978-3-642-14279-6CrossRefGoogle Scholar
Frankl, P. and Rödl, V., Near perfect coverings in graphs and hypergraphs. European J. Combin. 6(1985), 317–326. https://doi.org/10.1016/S0195-6698(85)80045-7CrossRefGoogle Scholar
Jing, Y. and Mohar, B., The genus of complete 3-uniform hypergraphs. J. Combin. Theory Ser. B 141(2020), 223–239. https://doi.org/10.1016/j.jctb.2019.08.002CrossRefGoogle Scholar
Jing, Y. and Mohar, B., Efficient polynomial-time approximation scheme for the genus of dense graphs. In: 59th Annual IEEE Symposium on Foundations of Computer Science—FOCS 2018. IEEE Computer Soc., Los Alamitos, CA, 2018, pp. 719–730.Google Scholar
Mohar, B. and Thomassen, C., Graphs on surfaces. Johns Hopkins Studies in the Mathematical Sciences, Johns Hopkins University Press, Baltimore, MD, 2001.Google Scholar
Parsons, T. D., Pica, G., Pisanski, T., and Ventre, A. G. S., Orientably simple graphs. Math. Slovaca 37(1987), 391–394.Google Scholar
Pippenger, N. and Spencer, J., Asymptotic behavior of the chromatic index for hypergraphs. J. Combin. Theory Ser. A 51(1989), 24–42. https://doi.org/10.1016/0097-3165(89)90074-5CrossRefGoogle Scholar
Ringel, G., Das Geschlecht des vollständigen paaren Graphen. Abh. Math. Sem. Univ. Hamburg 28(1965), 139–150. https://doi.org/10.1007/BF02993245CrossRefGoogle Scholar
Ringel, G. and Youngs, J. W. T., Solution of the Heawood map-coloring problem. Proc. Natl Acad. Sci. USA 60(1968), 438–445. https://doi.org/10.1073/pnas.60.2.438CrossRefGoogle ScholarPubMed
Rödl, V. and Thomas, R., On the genus of a random graph. Random Structures Algorithms 6(1995), 1–12. https://doi.org/10.1002/rsa.3240060102CrossRefGoogle Scholar
Stahl, S., On the average genus of the random graph. J. Graph Theory 20(1995), 1–18. https://doi.org/10.1002/jgt.3190200102CrossRefGoogle Scholar
Thomassen, C., The graph genus problem is NP-complete. J. Algorithms 10(1989), 568–576. https://doi.org/10.1016/0196-6774(89)90006-0CrossRefGoogle Scholar
Youngs, J. W. T., Minimal imbeddings and the genus of a graph. J. Math. Mech. 12(1963), 303–315.Google Scholar