Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T06:35:13.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Spectra and Commensurability

Published online by Cambridge University Press:  20 November 2018

D. B. McReynolds
D. B. McReynolds*
Affiliation:
Purdue University, West Lafayette, IN 47906, USA. e-mail: dmcreyno@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The work of Reid, Chinburg–Hamilton–Long–Reid, Prasad–Rapinchuk, and the author with Reid have demonstrated that geodesics or totally geodesic submanifolds can sometimes be used to determine the commensurability class of an arithmetic manifold. The main results of this article show that generalizations of these results to other arithmetic manifolds will require a wide range of data. Specifically, we prove that certain incommensurable arithmetic manifolds arising from the semisimple Lie groups of the form 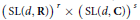${{\left( \text{SL(d,}\,\mathbf{R}) \right)}^{r}}\,\times \,{{\left( \text{SL(d,}\,\mathbf{C}) \right)}^{s}}$ have the same commensurability classes of totally geodesic submanifolds coming from a fixed field. This construction is algebraic and shows the failure of determining, in general, a central simple algebra from subalgebras over a fixed field. This, in turn, can be viewed in terms of forms of 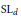$\text{S}{{\text{L}}_{d}}$ and the failure of determining the form via certain classes of algebraic subgroups.

Keywords

20G25arithmetic groupsBrauer groupsarithmetic equivalencelocally symmetric manifolds
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 184 - 197
Copyright
Copyright © 2013

References

[1] Aka, M., Arithmetic groups with isomorphic finite quotients. J. Algebra 352(2012), 322–340.http://dx.doi.org/10.1016/j.jalgebra.2011.10.033 Google Scholar
[2] Borel, A. and Harish-Chandra, , Arithmetic subgroups of algebraic groups. Ann. of Math. (2)75(1962), 485–535. http://dx.doi.org/10.2307/1970210 Google Scholar
[3] Cassels, J.W. S. and Frölich, A., Algebraic number theory. London Mathematical Society, 1967.Google Scholar
[4] Chernousov, V. I., Rapinchuk, A. S., and Rapinchuk, I. A., On the genus of a division algebra. C. R. Math. Acad. Sci. Paris 350(2012), 17–18. http://dx.doi.org/10.1016/j.crma.2012.09.014 Google Scholar
[5] Chinburg, T., Hamilton, E., Long, D. D., and Reid, A.W., Geodesics and commensurability classes of arithmetic hyperbolic 3-manifolds. Duke Math. J. 145(2008), 25–44.http://dx.doi.org/10.1215/00127094-2008-045 Google Scholar
[6] Cox, B., Linowitz, B., McReynolds, D. B., and Miller, N., Local invariants and Galois cohomology. In preparation.Google Scholar
[7] Garibaldi, S. and Saltman, D., Quaternion algebras with the same subfields. In: Quadratic forms, linear algebraic groups, and cohomology, Dev. Math. 18, Springer, New York, 2010, 225–238.Google Scholar
[8] Komatsu, K., On the adèle rings of algebraic number fields. KodaiMath. Sem. Rep. 28(1976), 78–84.http://dx.doi.org/10.2996/kmj/1138847384 Google Scholar
[9] Komatsu, K., On the adèle rings and zeta-functions of algebraic number fields. Kodai Math. J. 1(1978), 394–400. http://dx.doi.org/10.2996/kmj/1138035648 Google Scholar
[10] Komatsu, K., On adèle rings of arithmetically equivalent fields. Acta Arith. 43(1984), 93–95.Google Scholar
[11] Linowitz, B., Isospectral towers of Riemannian Manifolds. New York J. Math. 18(2012), 451–461.Google Scholar
[12] Lubotzky, A., Samuels, B., and Vishne, U., Division Algebras and Non-Commensurable Isospectral Manifolds. Duke Math. J. 135(2006), 361–379.http://dx.doi.org/10.1215/S0012-7094-06-13525-1 Google Scholar
[13] Marcus, D. A., Number fields. Springer–Verlag, New York–Heidelberg, 1977.Google Scholar
[14] McReynolds, D. B. and Reid, A.W., The genus spectrum of hyperbolic 3-manifolds. Math. Res. Lett.,to appear.Google Scholar
[15] Meyer, J., Division algebras with infinite genus. Preprint.Google Scholar
[16] Perlis, R., On the equation ζK(s) = ζK’ (s). J. Number Theory 9(1977), 342–360.http://dx.doi.org/10.1016/0022-314X(77)90070-1 Google Scholar
[17] Pierce, R. S., Associative algebras. Grad. Texts in Math. 88, Springer-Verlag, New York–Berlin, 1982.Google Scholar
[18] Platonov, V. and Rapinchuk, A., Algebraic groups and number theory. Pure Appl. Math. 139, Academic Press, Boston, MA, 1994.Google Scholar
[19] Prasad, G. and Rapinchuk, A., Weakly commensurable arithmetic groups and isospectral locally symmetric spaces. Publ. Math. Inst. Hautes Étud. Sci. 109(2009), 113–184.Google Scholar
[20] Reid, A. W., Isospectrality and commensurability of arithmetic hyperbolic 2- and 3-manifolds. Duke Math. J. 65(1992), 215–228.http://dx.doi.org/10.1215/S0012-7094-92-06508-2 Google Scholar
[21] Serre, J.-P., Local fields. Grad. Texts in Math. 67, Springer-Verlag, New York–Berlin, 1979.Google Scholar
[22] Witte-Morris, D., Introduction to arithmetic groups. http://people.uleth.ca/_dave.morris/books/IntroArithGroups.pdf Google Scholar