Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T06:23:01.984Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometric Study of Minkowski Differences of Plane Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Yves Martinez-Maure
Yves Martinez-Maure*
Affiliation:
1, rue Auguste Perret, F-92500 Rueil-Malmaison, France e-mail: martinezmaure@aol.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the Euclidean plane 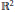${{\mathbb{R}}^{2}}$, we define the Minkowski difference 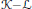$\mathcal{K}-\mathcal{L}$ of two arbitrary convex bodies 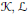$\mathcal{K},\mathcal{L}$ as a rectifiable closed curve 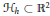${{\mathcal{H}}_{h}}\subset {{\mathbb{R}}^{2}}$ that is determined by the difference 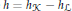$h={{h}_{K}}-{{h}_{\mathcal{L}}}$ of their support functions. This curve 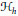${{\mathcal{H}}_{h}}$ is called the hedgehog with support function 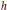$h$. More generally, the object of hedgehog theory is to study the Brunn–Minkowski theory in the vector space of Minkowski differences of arbitrary convex bodies of Euclidean space 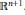${{\mathbb{R}}^{n+1}}$, defined as (possibly singular and self-intersecting) hypersurfaces of 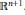${{\mathbb{R}}^{n+1}}$. Hedgehog theory is useful for: (i) studying convex bodies by splitting them into a sum in order to reveal their structure; (ii) converting analytical problems into geometrical ones by considering certain real functions as support functions. The purpose of this paper is to give a detailed study of plane hedgehogs, which constitute the basis of the theory. In particular: (i) we study their length measures and solve the extension of the Christoffel–Minkowski problem to plane hedgehogs; (ii) we characterize support functions of plane convex bodies among support functions of plane hedgehogs and support functions of plane hedgehogs among continuous functions; (iii) we study the mixed area of hedgehogs in 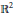${{\mathbb{R}}^{2}}$ and give an extension of the classical Minkowski inequality (and thus of the isoperimetric inequality) to hedgehogs.

Keywords

52A3052A1053A0452A3852A3952A40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 3 , 01 June 2006 , pp. 600 - 624
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Barbier, E., Note sur le probleme de l’aiguille et le jeu joint couvert. J. Math. Pures Apple. 5(1860), 273–286.Google Scholar
[2] Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper. Springer, Berlin. Reprint: Chelsea Publishing, New York, 1948.Google Scholar
[3] Geppert, H., Über den Brunn-Minkowskischen Satz. Math. Z. 42(1937), 238–254.Google Scholar
[4] Görtler, H., Erzeugung stützbarer Bereiche. I. Deutsche Math. 2(1937), 454–456.Google Scholar
[5] Görtler, H., Erzeugung stützbarer Bereiche. II. Deutsche Math. 3(1937), 189–200.Google Scholar
[6] Kallay, M., Reconstruction of a plane convex body from the curvature of its boundary. Israel J. Math. 17(1974), 149–161.Google Scholar
[7] Langevin, R., Levitt, G., and Rosenberg, H., Hérissons et multihérissons (enveloppes paramétrées par leur application de Gauss). In: Singularities, Banach Center Publ. 20, PWN, Warsaw, 1988, pp. 245–253.Google Scholar
[8] Martinez-Maure, Y., Feuilletages des surfaces et hérissons dans ℝ3 . Thèse de doctorat de 3ème cycle, Université Paris 7, 1985.Google Scholar
[9] Martinez-Maure, Y., A note on the tennis ball theorem. Amer. Math. Monthly 103(1996), 338–340.Google Scholar
[10] Martinez-Maure, Y., Sur les hérissons projectifs (enveloppes paramétrées par leur application de Gauss). Bull. Sci. Math. 121(1997), no. 8, 585–601.Google Scholar
[11] Martinez-Maure, Y., Hedgehogs of constant width and equichordal points. Ann. Polon. Math. 67(1997), no. 3, 285–288.Google Scholar
[12] Martinez-Maure, Y., De nouvelles inégalités géométriques pour les hérissons. Arch. Math. (Basel) 72(1999), 444–453.Google Scholar
[13] Martinez-Maure, Y., Indice d’un hérisson: étude et applications. Publ. Mat. 44(2000), 237–255.Google Scholar
[14] Martinez-Maure, Y., A fractal projective hedgehog. Demonstratio Math. 34(2001), no. 1, 59–63.Google Scholar
[15] Martinez-Maure, Y., Contre-exemple à une caractérisation conjecturée de la sphère. C. R. Acad. Sci. Paris, Sér. I Math. 332(2001), 41–44.Google Scholar
[16] Martinez-Maure, Y., Hedgehogs and zonoids. Adv. Math. 158(2001), 1–17.Google Scholar
[17] Martinez-Maure, Y., La théorie des hérissons (différences de corps convexes) et ses applications. Habilitation, Univ. Paris 7, 2001.Google Scholar
[18] Martinez-Maure, Y., Sommets et normales concourantes des courbes convexes de largeur constante et singularités des hérissons. Arch. Math. 79(2002) 489–498.Google Scholar
[19] Martinez-Maure, Y., Voyage dans l’univers des hérissons. In: Ateliers Mathematica, Paris, Vuibert, 2003, 445–470.Google Scholar
[20] Martinez-Maure, Y., Théorie des hérissons et polytopes. C. R. Acad. Sci. Paris Sér. I Math. 336(2003), no. 3, 241–244.Google Scholar
[21] Martinez-Maure, Y., Les multihérissons et le théorème de Sturm–Hurwitz. Arch. Math. (Basel) 80(2003), 79–86.Google Scholar
[22] Martinez-Maure, Y., A Brunn-Minkowski theory for minimal surfaces. Illinois J. Math 48(2004), no. 2, 589–607.Google Scholar
[23] Ohtsuka, H., Dirichlet problems of Riemann surfaces and conformal mappings. Nagoya Math. J. 3(1951), 91–137.Google Scholar
[24] Schneider, R., Convex Bodies: The Brunn-Minkowski Theory. Encyclopedia of Mathematics and Its Applications 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[25] Valentine, F. A., Convex Sets. McGraw-Hill, New York, 1964.Google Scholar