Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T04:19:26.152Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Actions and Codes

Published online by Cambridge University Press:  20 November 2018

V. Puppe
V. Puppe*
Affiliation:
Fachbereich Mathematik und Statistik, Universität Konstanz, 78457 Konstanz, Germany. email: Volker.Puppe@uni-konstanz.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A 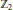${{\mathbb{Z}}_{2}}$-action with “maximal number of isolated fixed points” (i.e., with only isolated fixed points such that 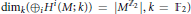${{\dim}_{k}}\left( {{\oplus }_{i}}{{H}^{i}}\left( M;k \right) \right)\,\,=\,\,\left| {{M}^{{{\mathbb{Z}}_{2}}}} \right|,\,k\,=\,\left. {{\mathbb{F}}_{2}} \right)$ on a 3-dimensional, closed manifold determines a binary self-dual code of 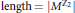$\text{length}\,\text{=}\,\left| {{M}^{{{\mathbb{Z}}_{2}}}} \right|$. In turn this code determines the cohomology algebra 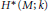${{H}^{*}}\,\left( M;k \right)$ and the equivariant cohomology 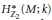$H_{{{\mathbb{Z}}_{2}}}^{*}\,\left( M;k \right)$. Hence, from results on binary self-dual codes one gets information about the cohomology type of 3-manifolds which admit involutions with maximal number of isolated fixed points. In particular, “most” cohomology types of closed 3-manifolds do not admit such involutions. Generalizations of the above result are possible in several directions, e.g., one gets that “most” cohomology types (over 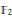${{\mathbb{F}}_{2}}$) of closed 3-manifolds do not admit a non-trivial involution.

Keywords

55M3557M6094B0505E20Involutions3-manifoldscodes
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 1 , 01 February 2001 , pp. 212 - 224
Copyright
Copyright © Canadian Mathematical Society 2001

References

[AP] Allday, C. and Puppe, V., Cohomological Methods in Transformation Groups. Cambridge Studies in Advanced Math. 32, Cambridge University Press, Cambridge, 1993.Google Scholar
[CP] Conway, J. H. and Pless, V., On the enumeration of self-dual codes. J. Combin. Theory Ser. A 28(1980), 26–53.Google Scholar
[CPS] Conway, J. H.,V. Pless and Sloane, N. J. A., The binary self-dual codes of length up to 32: A revised enumeration. J. Combin. Theory Ser. A 60(1992), 183–195.Google Scholar
[MH] Milnor, J. and Husemoller, D., Symmetric Bilinear Forms. Springer, Berlin, Heidelberg, New York, 1973.Google Scholar
[Pi] Pietsch, M., Involutionen und Codes. Diplomarbeit, Konstanz, 1999.Google Scholar
[Pl] Pless, V., A Classification of Self-Orthogonal Codes over GF(2). Discrete Math. 3(1972), 209–246.Google Scholar
[PS1] V. Pless and Sloane, N. J. A., Binary self-dual codes of length 24. Bull. Amer.Math. Soc. 80(1974), 1173–1178.Google Scholar
[PS2] V. Pless and Sloane, N. J. A., On the Classification and Enumeration of Self-Dual Codes. J. Combin. Theory Ser.A 18(1975), 313–335.Google Scholar
[Po] Postnikov, M. M., Construction of Intersectionrings of 3-dimensional Manifolds (Russian). Dokl. Akad. Nauk SSSR 61(1948), 795–797.Google Scholar
[Pu1] Puppe, V., Deformations of algebras and cohomology of fixed point sets. Manuscripta Math. (1979), 119–136.Google Scholar
[Pu2] Puppe, V., Simply Connected 6-Dimensional Manifolds with Little Symmetry and Algebras with Small Tangent Space. In: Prospects in Topology, (ed. Quinn, F.), Annals of Math. Studies 138, Princeton University Press, Princeton, 1995, 283–302.Google Scholar
[S] Sah, C.-H., Alternating and symmetric multilinear forms and Poincaré algebras. Comm. Algebra (2) 2(1974), 91–116.Google Scholar
[W] Wall, C. T. C., 1970: Surgery on Compact Manifolds. Academic Press, New York, 1970.Google Scholar