Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T07:12:10.780Z Has data issue: false hasContentIssue false
  • English
  • Français

The Groups of Regular Complex Polygons

Published online by Cambridge University Press:  20 November 2018

D. W. Crowe
D. W. Crowe*
Affiliation:
University College, IbadantNigeria
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The two-dimensional unitary space, U2, is a complex vector space of points (x, y) = (x1 + ix2, y1 + iy2), for which the distance between (x, y) and (x', y') is defined by 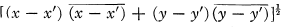. A unitary transformation is a linear transformation which preserves distance. A line is the set of points (x, y) satisfying some complex equation ax + by = c. A unitary transformation is a (unitary) reflection if it is of finite period n > 1 and leaves a line pointwise invariant. Thus à unitary matrix represents a reflection if its two characteristic roots are 1 and a complex nth root (n > 1) of 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 149 - 156
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Coxeter, H. S. M., The binary polyhedral groups and other generalizations of the quaternion group, Duke Math. J., 7 (1940), 367–379.Google Scholar
2. Coxeter, H. S. M., Quaternions and reflections, Amer. Math. Monthly, 53 (1946), 136–146.Google Scholar
3. Coxeter, H. S. M., Regular polytopes (London, 1948).Google Scholar
4. Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete groups (Berlin, 1957).Google Scholar
5. Goursat, E., Sur les substitutions orthogonales et les divisions régulières de Vespace, Ann. Sci. Ecole Norm. Sup. (3), 6 (1889), 9–102.Google Scholar
6. Seifert, H. and Threlfall, W., Topologische Untersuchungen der Diskontinuitdtsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphàrischen Raumes, Math. Ann., 104 (1931), 1–70.Google Scholar
7. Shephard, G. C., Regular complex polygons, Proc. London Math. Soc. (3), 2 (1952), 82–97.Google Scholar
8. Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Can. J. Math., 6 (1954), 274–304.Google Scholar