Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T07:46:20.558Z Has data issue: false hasContentIssue false
  • English
  • Français

The Heat Kernel and Green's Function on a Manifold with Heisenberg Group as Boundary

Published online by Cambridge University Press:  20 November 2018

Yilong Ni
Yilong Ni*
Affiliation:
Department of Mathematics and Statistics, McMaster University, 1280 Main StreetWest, Hamilton, ON, L8S 4K1 e-mail: yilong.ni@aya.yale.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the Riemannian Laplace-Beltrami operator $L$ on a Riemannian manifold with Heisenberg group 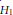${{H}_{1}}$ as boundary. We calculate the heat kernel and Green's function for $L$, and give global and small time estimates of the heat kernel. A class of hypersurfaces in this manifold can be regarded as approximations of 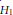${{H}_{1}}$. We also restrict $L$ to each hypersurface and calculate the corresponding heat kernel and Green's function. We will see that the heat kernel and Green's function converge to the heat kernel and Green's function on the boundary.

Keywords

35H2058J9953C17Heisenberg groupheat kernel
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 3 , 01 June 2004 , pp. 590 - 611
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Beals, R., Geometry and PDE on the Heisenberg group: a case study. Geometrical Study of Differential Equations, ContemporaryMath. 285, Amer. Math. Soc., Providence, 2001, 21–27.Google Scholar
[2] Beals, R., Gaveau, B. and Greiner, P. C., Hamilton-Jacobi theory and the heat kernel on Heisenberg groups. J. Math. Pures Appl. (7) 79(2000), 633–689.Google Scholar
[3] Folland, G. B., A fundamental solution for a subelliptic operator. Bull. Amer. Math. Soc. 79(1973), 373–376.Google Scholar
[4] Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous-elliptiques sur certains groupes nilpotents. Acta Math. 139(1977), 95–153.Google Scholar
[5] Hulanicki, A., The distribution of energy in the Brownian motion in the Gaussian field and analytic-hypoellipticity of certain subelliptic operators on the Heisenberg group. Studia Math. 56(1976), 165–173.Google Scholar
[6] Ni, Y., Geodesics in a manifold with Heisenberg group as boundary. Canad. J. Math. 56(2004), 566–589.Google Scholar