Hostname: page-component-7f64f4797f-pmsz9 Total loading time: 0 Render date: 2025-11-04T14:15:11.966Z Has data issue: false hasContentIssue false
  • English
  • Français

Heegner Points and the Rank of Elliptic Curves over Large Extensions of Global Fields

Published online by Cambridge University Press:  20 November 2018

Florian Breuer  and
Bo-Hae Im
Florian Breuer
Affiliation:
Department of Mathematical Sciences, University of Stellenbosch, Stellenbosch 7600, South Africa e-mail:, fbreuer@sun.ac.za
Bo-Hae Im
Affiliation:
Department of Mathematics, Chung-Ang University, 221 Haukseok-dong, Dongjak-gu, Seoul 156-756, South Korea e-mail:, imbh@cau.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 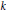$k$ be a global field, 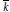$\bar{k}$ a separable closure of 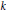$k$ , and 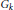${{G}_{k}}$ the absolute Galois group Gal 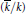$(\bar{k}/k)$ of 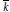$\bar{k}$ over 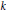$k$ . For every 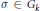$\sigma \,\in \,{{G}_{K}}$ , let 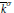${{\bar{k}}^{\sigma }}$ be the fixed subfield of 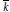$\bar{k}$ under $\sigma$ . Let 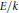$E/k$ be an elliptic curve over 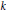$k$ . It is known that the Mordell–Weil group 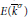$E({{\bar{k}}^{\sigma }})$ has infinite rank. We present a new proof of this fact in the following two cases. First, when 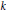$k$ is a global function field of odd characteristic and 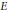$E$ is parametrized by a Drinfeld modular curve, and secondly when 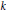$k$ is a totally real number field and 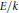$E/k$ is parametrized by a Shimura curve. In both cases our approach uses the non-triviality of a sequence of Heegner points on 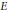$E$ defined over ring class fields.

Keywords

11G05

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 3 , 01 June 2008 , pp. 481 - 490
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Breuer, F., Higher Heegner points on elliptic curves over function fields. J. Number Theory 104(2004), no. 2, 315–326.Google Scholar
[2] Breuer, F., Images of isogeny classes on modular elliptic curves. Math. Res. Lett. 11(2004), no. 5-6, 649–651.Google Scholar
[3] Breuil, C., Conrad, B., Diamond, F., and Taylor, R., On the modularity of elliptic curves over Q: wild 3-adic exercises. J. Amer. Math. Soc. 14(2001), no. 4, 843–939.Google Scholar
[4] Brown, M. L., Heegner Modules and Elliptic Curves, Lecture Notes in Mathematics 1849, Springer-Verlag, Berlin, 2000.Google Scholar
[5] Faltings, G., Endlichkeitssätze für abelsche Varietäten über Zahlkörpern. Invent.Math. 73(1983), no. 3, 349–366.Google Scholar
[6] Fried, M. and Jarden, M., Field Arithmetic. Second edition. Ergebnisse derMathematik und ihrer Grenzgebiete 11, Springer-Verlag, Berlin, 2005.Google Scholar
[7] Gekeler, E.-U. and Reversat, M., Jacobians of Drinfeld modular curves. J. Reine Angew.Math. 476(1996), 27–93.Google Scholar
[8] Geyer, W.-D. and Jarden, M., The rank of abelian varieties over large algebraic fields. Arch. Math. (Basel) 86(2006), no. 3, 211–216.Google Scholar
[9] Im, B., Mordell–Weil groups and the rank of elliptic curves over large fields. Canad. J. Math. 58(2006), no. 4 (2006), 796–819.Google Scholar
[10] Im, B., The rank of elliptic curves with 2-torsion points over large fields. Proc. Amer. Math. Soc. 134(2006), no. 6, 1623–1630.Google Scholar
[11] Im, B., Heegner points and the rank of elliptic curves over large fields. Trans. Amer.Math. Soc. 359(2007), no. 12, 6143–6154.Google Scholar
[12] Im, B. and Larsen, M., Abelian varieties over cyclic fields. To appear in Amer. J. Math.Google Scholar
[13] Lang, S., Fundamentals of Diophantine Geometry. Springer-Verlag, New York, 1983.Google Scholar
[14] Larsen, M., Rank of elliptic curves over almost algebraically closed fields. Bull. LondonMath. Soc. 35(2003), no. 6, 817–820.Google Scholar
[15] Neukirch, J., “Algebraische Zahlentheorie”, Springer-Verlag, Berlin, 1992.Google Scholar
[16] Taylor, R. and A.Wiles, Ring-theoretic properties of certain Hecke algebras. Ann. of Math. 141(1995), no. 3, 553–572.Google Scholar
[17] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. 141(1995), no. 3, 443–551.Google Scholar
[18] Zhang, S., Heights of Heegner points on Shimura curves. Ann. of Math. 153(2001), no. 1, 27–147.Google Scholar