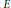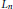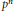Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Delbourgo, Daniel
and
Lei, Antonio
2017.
Estimating the growth in Mordell–Weil ranks and Shafarevich–Tate groups over Lie extensions.
The Ramanujan Journal,
Vol. 43,
Issue. 1,
p.
29.
Delbourgo, Daniel
and
Chao, Qin
2019.
$$\hbox {K}_{1}$$ K 1 -congruences for three-dimensional Lie groups.
Annales mathématiques du Québec,
Vol. 43,
Issue. 1,
p.
161.
DELBOURGO, DANIEL
2021.
Variation of the algebraic λ-invariant over a solvable extension.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 170,
Issue. 3,
p.
499.
Lim, Meng Fai
2022.
On order of vanishing of characteristic elements.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Shnidman, Ari
and
Weiss, Ariel
2023.
Rank growth of elliptic curves over 𝑁-th root extensions.
Transactions of the American Mathematical Society, Series B,
Vol. 10,
Issue. 16,
p.
482.
Kellock, Lilybelle Cowland
and
Dokchitser, Vladimir
2023.
Root numbers and parity phenomena.
Bulletin of the London Mathematical Society,
Vol. 55,
Issue. 6,
p.
2557.