Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T13:48:42.268Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Dimensional Asymptotic Cycles

Published online by Cambridge University Press:  20 November 2018

Sol Schwartzman
Sol Schwartzman*
Affiliation:
Department of Mathematics, University of Rhode Island, Kingston, Rhode Island 02881, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a 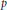$p$-dimensional oriented foliation of an $n$-dimensional compact manifold 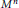${{M}^{n}}$ and a transversal invariant measure $\tau$, Sullivan has defined an element of 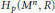${{H}_{p}}\left( {{M}^{n}},\,R \right)$. This generalized the notion of a $\mu$-asymptotic cycle, which was originally defined for actions of the real line on compact spaces preserving an invariant measure $\mu$. In this one-dimensional case there was a natural 1–1 correspondence between transversal invariant measures $\tau$ and invariant measures $\mu$ when one had a smooth flow without stationary points.

For what we call an oriented action of a connected Lie group on a compact manifold we again get in this paper such a correspondence, provided we have what we call a positive quantifier. (In the one-dimensional case such a quantifier is provided by the vector field defining the flow.) Sufficient conditions for the existence of such a quantifier are given, together with some applications.

Keywords

57R3057S20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 3 , 01 June 2003 , pp. 636 - 648
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bourbaki, N., Éléments de mathématique. Livre VI: Intégration. Chapitre 6. Paris, Hermann, 1959, 58.Google Scholar
[2] Bredon, Glen, Introduction to Compact Transformation Groups. Academic Press, 1972.Google Scholar
[3] Connes, Alain, Noncommutative Geometry. Academic Press, 1994.Google Scholar
[4] Ruelle, David and Sullivan, Dennis, Currents, Flows and Diffeomorphisms. Topology (4) 14(1975), 319.Google Scholar
[5] Schwartzman, Sol, Asymptotic Cycles. Annals of Math. 66(1957), 270.Google Scholar
[6] Sullivan, Dennis, Dynamical Study of Foliated Manifolds and Complex Manifolds. Invent. Math. 36(1976), 225.Google Scholar