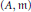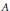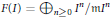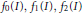Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhu, Guangjun
2009.
Fiber Coefficients and Depth of Fiber Cones.
Communications in Algebra,
Vol. 37,
Issue. 10,
p.
3686.
Zhu, Guangjun
2011.
Primary Ideals with Good Fiber Cone.
Communications in Algebra,
Vol. 39,
Issue. 7,
p.
2276.
Jayanthan, A. V.
and
Nanduri, Ramakrishna
2014.
On the depth of fiber cones of stretched m-primary ideals.
Indian Journal of Pure and Applied Mathematics,
Vol. 45,
Issue. 6,
p.
925.
D’Cruz, Clare
and
Guerrieri, Anna
2019.
Homology, mixed multiplies and Hilbert coefficients of the fiber cone.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 04,
p.
1950061.
Jorge Pérez, V.H.
and
Lima, P.H.
2022.
Coefficient ideals of the fiber cone.
Bulletin des Sciences Mathématiques,
Vol. 180,
Issue. ,
p.
103191.