Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T13:42:28.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Hölder Compactification for Some Manifolds with Pinched Negative Curvature Near Infinity

Published online by Cambridge University Press:  20 November 2018

Eric Bahuaud  and
Tracey Marsh
Eric Bahuaud
Affiliation:
Department of Mathematics, University of Washington, Seattle, Washington 98195, U.S.A. e-mail:ebahuaud@math.univ-montp2.fr , marsh tracey@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

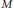We consider a complete noncompact Riemannian manifold $M$ and give conditions on a compact submanifold 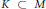$K\,\subset \,M$ so that the outward normal exponential map off the boundary of 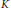$K$ is a diffeomorphism onto 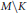$M\backslash K$. We use this to compactify 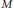$M$ and show that pinched negative sectional curvature outside 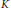$K$ implies 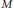$M$ has a compactification with a well-defined Hölder structure independent of 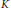$K$. The Hölder constant depends on the ratio of the curvature pinching. This extends and generalizes a 1985 result of Anderson and Schoen.

Keywords

53C20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 6 , 01 December 2008 , pp. 1201 - 1218
Copyright
Copyright © Canadian Mathematical Society 2008

References

[AS85] Anderson, M. T. and Schoen, R., Positive harmonic functions on complete manifolds of negative curvature. Ann. of Math. 121(1985), no. 3, 4219–461.Google Scholar
[EO73] Eberlein, P. and O’Neill, B., Visibility manifolds. Pacific J. Math. 46(1973), 45–109.Google Scholar
[Kli95] Klingenberg, W. P. A., Riemannian Geometry. Second edition. de Gruyter Studies in Mathematics 1,Walter de Gruyter, Berlin, 1995.Google Scholar
[Pet98] Petersen, P., Riemannian Geometry. Graduate Texts inMathematics 171, Springer-Verlag, New York, 1998.Google Scholar