Published online by Cambridge University Press: 20 November 2018
Let 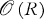 denote the space of functions holomorphic on an open Riemann surface R, where
denote the space of functions holomorphic on an open Riemann surface R, where 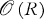 has the topology of uniform convergence on compact sets. In this note, we characterize the dual space
has the topology of uniform convergence on compact sets. In this note, we characterize the dual space 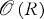 *. The result is not new, for it is implicitly contained in the more general results of Tillmann [5] and, in case R is planar, in those of Köthe [4]. However, the paper of Gunning and Narasimhan [3], which appeared subsequently, allows us to give a short proof of this important result. Actually, our characterization is a natural one in terms of differentials, while the Köthe-Tillmann characterization is in terms of functions, but we show that these two characterizations are isomorphic. We end our paper by using our characterization to prove an interpolation result. The second author gratefully acknowledges a helpful discussion with Professor George Szekeres.
*. The result is not new, for it is implicitly contained in the more general results of Tillmann [5] and, in case R is planar, in those of Köthe [4]. However, the paper of Gunning and Narasimhan [3], which appeared subsequently, allows us to give a short proof of this important result. Actually, our characterization is a natural one in terms of differentials, while the Köthe-Tillmann characterization is in terms of functions, but we show that these two characterizations are isomorphic. We end our paper by using our characterization to prove an interpolation result. The second author gratefully acknowledges a helpful discussion with Professor George Szekeres.