Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:08:50.043Z Has data issue: false hasContentIssue false
  • English
  • Français

Homology of Abelian Coverings of Links and Spatial Graphs

Published online by Cambridge University Press:  20 November 2018

Makoto Sakuma
Makoto Sakuma*
Affiliation:
Department of Mathematics Faculty of Science Osaka University Toyonaka, Osaka 560 Japan e-mail: sakuma@math.wani.osaka-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

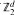We give (1) a formula of the first Betti numbers of abelian coverings of links in terms of the Alexander ideals, (2) certain estimates of the orders of the torsion parts of their first homology groups in terms of the Alexander polynomials, and (3) a structure theorem of the first homology groups of -coverings of spatial graphs. As an application, we generalize a result of E. Hironaka on polynomial periodicity of the first Betti numbers in certain towers of abelian coverings of complex surfaces.

Keywords

57M0557M1257M25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 1 , 01 February 1995 , pp. 201 - 224
Copyright
Copyright © Canadian Mathematical Society 1995

References

[Bo] Bourbaki, N., Commutative algebra, Hermann-Addison Wesley, Paris-Reading, 1972.Google Scholar
[Br] Bredon, G., Introduction to compact transformation groups, Academic Press, London, New York, 1972.Google Scholar
[BZ] Burde, G. and Zieschang, H., Knots, de Gruyter Stud. Math. 5, Walter de Gruyter, Berlin, New York, 1985.Google Scholar
[F] Fox, R.H., Free differential calculus III, Ann. of Math. 59(1954), 195–210.Google Scholar
[Ge] Goeritz, L., Die Betti'schen Zahlen der zyklishen Überlagerungsràume der Knotenausserdume, Amer. J. Math. 56(1934), 194–198.Google Scholar
[GS] Gonz, F.ález-Acuña and Short, H., Cyclic branched coverings of knots and homology spheres, Rev. Mat. Univ. Complut. Madrid 4(1992), 97–120.Google Scholar
[Gr] McA. Gordon, C., Knots whose branched cyclic covering have periodic homology, Trans. Amer. Math. Soc. 168(1972), 357–370.Google Scholar
[GL] Gordon, C.McA. and Litherland, R.A., On the signature of a link, Invent. Math. 47(1978), 53–69.Google Scholar
[He] Hempel, J., Homology of branched coverings of, 3 -manifolds, Canad. J. Math. 44(1992), 119–134.Google Scholar
[HI1] Hillman, J.A., Alexander ideals of links, Lecture Notes in Math. 895, Springer-Verlag, Berlin, Heiderberg, New York, 1981.Google Scholar
[H12] Hillman, J.A., New proofs of two theorems on periodic knots, Arch. Math. 37(1981), 457–461.Google Scholar
[Hrl] Hironaka, E., Polynomial periodicity for Betti numbers of covering surfaces, Invent. Math. 108(1992), 289–321.Google Scholar
[Hr2] Hironaka, E., Intersection theory on branched covering surfaces and polynomial periodicity, Internat. Math. Res. Notices 6(1993), 185–196.Google Scholar
[HK] Hosokawa, F. and Kinoshita, S., On the homology group of branched cyclic covering spaces of links,, Osaka J. Math. 12(1960), 331–335.Google Scholar
[LI] Libgober, A., Alexander polynomial of plane algebraic curves and cyclic multiple planes, Duke Math. J. 49(1982), 833–851.Google Scholar
[L2] Libgober, A., On the homology of finite abelian coverings, Topology Appl. 43(1992), 157–166.Google Scholar
[MM] Mayberry, J.P. and Murasugi, K., Torsion groups of abelian coverings of links, Trans. Amer. Math. Soc. 271(1982), 143–173.Google Scholar
[NT] Nagao, H. and Tsushima, Y., Representations of finite groups, Academic Press, 1989.Google Scholar
[Nkl] Nakao, M., On the ℤ2 ⊕ ℤ2 branched coverings of spatial 0-graphs, Kobe J. Math. 9(1992), 89–99.Google Scholar
[Nk2] Nakao, M., On the ℤ2⊕ℤ2 branched coverings of spatial K4-curves. In: Knot 90, (ed. Kawauchi, A.), Walter de Gruyter Co., 1992. 103–116.Google Scholar
[Nm] Namba, M., Branched coverings and algebraic functions, Res. Notes Math. 161, Pitman-Longman, 1987.Google Scholar
[P] Plans, A., Aportacion al estudio de los grupos de homologia de los recubrimientos cicicos ramificados correspondiente a un nudo, Rev. Real Acad. Cienc. Exact. Fis. Natur. Madrid 47(1953), 161–193.Google Scholar
[Ri] Riley, R., Growth of order of homology of cyclic branched covers of knots, Bull. London Math. Soc. 22(1990), 287–297.Google Scholar
[Ro] Rolfsen, D., Knots and links, Publish or Perish Inc., 1976.Google Scholar
[Ski] Sakuma, M., The homology groups of abelian coverings of links, Math. Sem. Notes, Kobe Univ. 7(1979), 515–530.Google Scholar
[Sk2] Sakuma, M., On the polynomials of periodic links, Math. Ann. 257(1981), 487–494.Google Scholar
[Sr] Sarnak, P., Betti numbers of congruence groups, preprint.Google Scholar
[SS] Shinohara, Y. and Sumners, D.W., Homology invariants of cyclic coverings with applications to links,, Trans. Amer. Math. Soc. 163(1972), 101–121.Google Scholar
[Sul] Sumners, D.W., Polynomial invariants and the integral homology of coverings of knots and links, Invent. Math. 15(1972), 78–90.Google Scholar
[Su2] Sumners, D.W., On the homology of finite cyclic coverings of higher-dimensional links, Proc. Amer. Math. Soc. 46(1974), 143–149.Google Scholar
[T] Torres, G., On the Alexander polynomial, Ann. of Math. 57(1953), 57–89.Google Scholar
[VW] d, P.. Val and Weber, C., Plans’ theorem for links, Topology Appl. 34(1990), 247–255.Google Scholar
[W] Weber, C., Sur une formule de R.H. Fox concernant Thomologie des revetments cycliques, Enseign. Math. 25(1979), 261–271.Google Scholar
[Z] Zariski, O., On the topology of algebroid singularities, Amer. J. Math. 54(1932), 453–465.Google Scholar
[AR 90] Zariski, O., Classical Dirichlet forms on topological vector spaces: Closability and a Cameron-Martin formula, J. Funct. Anal. 88(1990), 395-136.Google Scholar
[AR 91] Zariski, O., Stochastic differential equations in infinite dimensions: Solutions via Dirichlet forms, Probab. Theory Related Fields 89(1991), 347-386.Google Scholar