Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:38:49.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Homology of Branched Coverings of 3-Manifolds

Published online by Cambridge University Press:  20 November 2018

John Hempel
John Hempel*
Affiliation:
Rice University Houston, Texas USA 77251, email: hempel@rice.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a relation between the homology groups H1(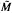) and H1 (M) for a branched cyclic cover 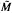→ M of arbitrary closed, oriented 3-manifolds which generalizes a classical result of Plans on covers of S3 branched over a knot and provides other quantitative information as well. We include a general "free calculus" procedure for computing homology groups of branched covers and reinterpret the results in this computational setting.

Keywords

57N1057M0557M12
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 1 , 01 December 1991 , pp. 119 - 134
Copyright
Copyright © Canadian Mathematical Society 1989

References

[CM] Valerio Chumillas and José Montesinos, The homology of cyclic and irregular dihedral coverings branched over homology spheres, Math. Ann. 280(1988), 483–500.Google Scholar
[F] Floyd, E.E., Orbit spaces of finite transformation groups I, Duke Math. J. 20(1953), 563–567..Google Scholar
[Fo] Fox, R.H., Free differential calculus V, The Alexander matrices re-examined, Ann. of Math. 71(1960), 408–422.Google Scholar
[Hi ] John Hempel, Intersection Calculus on Surfaces with Applications to 3-manifolds, Memoirs of the Amer. Math Soc. No. 282 43(1983), 1–48.Google Scholar
[H2] , Homology of coverings, Pacific J. Math. 112(1984), 83–113.Google Scholar
[H3] , Coverings of Dehn fillings of surface bundles, Topology and its applications 24(1986), 157–170.Google Scholar
[P] Plans, A., Aportacion al astudio de los grupos de homologia de los recubrimientos circlicos ramificados correspondientes a un nudo, Rev. Real Acad. Cienc. Exact. Fis. Natur. Madrid 47(1953), 161–193..Google Scholar
[dR] Rham, G. de, Sur I analysis situs des variétés à n dimensions, J. Math. Pures Appl. 10(1931), 115–200.Google Scholar
[VW] del Val, Pablo and Weber, Claude, Plans ‘ theorem for links, Topology and its Applications 34(1990), 247–255.Google Scholar