Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T06:55:23.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Homology TQFT's and the Alexander–Reidemeister Invariant of 3-Manifolds via Hopf Algebras and Skein Theory

Published online by Cambridge University Press:  20 November 2018

Thomas Kerler
Thomas Kerler*
Affiliation:
The Ohio State University, Department of Mathematics, 231 West 18th Avenue, Columbus, OH 43210, U.S.A. email: kerler@math.ohio-state.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop an explicit skein-theoretical algorithm to compute the Alexander polynomial of a 3-manifold from a surgery presentation employing the methods used in the construction of quantum invariants of 3-manifolds. As a prerequisite we establish and prove a rather unexpected equivalence between the topological quantum field theory constructed by Frohman and Nicas using the homology of 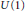$U\left( 1 \right)$-representation varieties on the one side and the combinatorially constructed Hennings TQFT based on the quasitriangular Hopf algebra 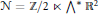$\mathcal{N=}\mathbb{Z}\text{/2}\ltimes {{\wedge }^{*}}{{\mathbb{R}}^{2}}$ on the other side. We find that both TQFT's are 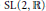$\text{SL}\left( 2,\,\mathbb{R} \right)$-equivariant functors and, as such, are isomorphic. The 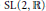$\text{SL}\left( 2,\,\mathbb{R} \right)$-action in the Hennings construction comes from the natural action on 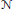$\mathcal{N}$ and in the case of the Frohman–Nicas theory from the Hard–Lefschetz decomposition of the 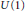$U\left( 1 \right)$-moduli spaces given that they are naturally Kähler. The irreducible components of this TQFT, corresponding to simple representations of 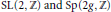$\text{SL}\left( 2,\,\mathbb{Z} \right)\,\text{and}\,\text{Sp}\left( 2g,\,\mathbb{Z} \right)$, thus yield a large family of homological TQFT's by taking sums and products. We give several examples of TQFT's and invariants that appear to fit into this family, such as Milnor and Reidemeister Torsion, Seiberg–Witten theories, Casson type theories for homology circles à la Donaldson, higher rank gauge theories following Frohman and Nicas, and the 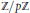$\mathbb{Z}/p\mathbb{Z}$ reductions of Reshetikhin–Turaev theories over the cyclotomic integers 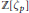$\mathbb{Z}[{{\zeta }_{p}}]$. We also conjecture that the Hennings TQFT for quantum-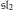$\mathfrak{s}{{\mathfrak{l}}_{2}}$ is the product of the Reshetikhin–Turaev TQFT and such a homological TQFT.

Keywords

Primary:57R56secondary:14D2016W3017B3718D3557M27
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 4 , 01 August 2003 , pp. 766 - 821
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Atiyah, M., Topological quantum field theories. Inst. Hautes Études Sci. Publ. Math. 68(1988), 175–186.Google Scholar
[2] Boden, H. and Nicas, A., Universal formulae for SU(n) Casson invariants of knots. Trans. Amer. Math. Soc. (7) 352(2000), 3149–3187.Google Scholar
[3] Bespalov, Yu., Kerler, T., Lyubashenko, V. and Turaev, V., Integrals for braided Hopf algebras. J. Pure Appl. Algebra (2) 148(2000), 113–164.Google Scholar
[4] Burde, G. and Zieschang, H., Knots. de Gruyter Stud. Math. 5, Walter de Gruyter, 1985.Google Scholar
[5] Donaldson, S. K., Topological field theories and formulae of Casson and Meng.Taubes. In: Proceedings of the Kirbyfest (Berkeley, CA, 1998), Geom. Topol. Monogr. 2(1999), 87–102 (electronic).Google Scholar
[6] Drinfeld, V. G., On almost cocommutative Hopf algebras. LeningradMath. J. (2) 1(1990), 321–342.Google Scholar
[7] Frohman, C., Unitary representations of knot groups. Topology (1) 32(1993), 121–144.Google Scholar
[8] Frohman, C. and Nicas, A., The Alexander Polynomial via topological quantum field theory. In: Differential Geometry, Global Analysis, and Topology, CMS Conf. Proc. 12, Amer. Math. Soc. Providence, RI, 1991, 27–40.Google Scholar
[9] Frohman, C. and Nicas, A., An intersection homology invariant for knots in a rational homology 3-sphere. Topology (1) 33(1994), 123–158.Google Scholar
[10] Fock, V. V. and Rosly, A. A., Moduli space of flat connections as a Poisson manifold. In: Advances in quantum field theory and statistical mechanics, 2nd Italian. Russian collaboration (Como, 1996), Internat. J. Modern Phys. B 11(1997), 3195–3206.Google Scholar
[11] Gilmer, P., Integrality for TQFTs. Preprint, 2001, math.QA/0105059.Google Scholar
[12] Goodman, R. and Wallach, N. R., Representations and invariants of the classical groups. Encyclopedia Math. Appl. 68, Cambridge University Press, 1998.Google Scholar
[13] Griffith, P. and Harris, J., Principles of algebraic geometry.Wiley Classics Library, John Wiley & Sons, Inc., New York, 1978 and 1994.Google Scholar
[14] Hennings, M., Invariants of links and 3-manifolds obtained from Hopf algebras. J. London Math. Soc. (2) 54(1996), 594–624.Google Scholar
[15] Kauffman, L. H. and Radford, D. E., Invariants of 3-manifolds derived from finite-dimensional Hopf algebras. J. Knot Theory Ramifications (1) 4(1995), 131–162.Google Scholar
[16] Kauffman, L. H., Gauss codes, quantum groups and ribbon Hopf algebras. Rev. Math. Phys. (4) 5(1993), 735–773.Google Scholar
[17] Kerler, T., Darstellungen der Quantengruppen und Anwendungen. Diploma thesis, ETH-Zürich, 1989, unpublished.Google Scholar
[18] Kerler, T., Mapping class group actions on quantum doubles. Comm.Math. Phys. 168(1994), 353–388.Google Scholar
[19] Kerler, T., Genealogy of nonperturbative quantum-invariants of 3-manifolds: The surgical family. In: Geometry and Physics, Lecture Notes in Pure and Appl. Physics 184, Marcel Dekker, 1997, 503.547.Google Scholar
[20] Kerler, T., On the connectivity of cobordisms and half-projective TQFT's. Comm. Math. Phys. (3) 198(1998), 535–590.Google Scholar
[21] Kerler, T., Bridged links and tangle presentations of cobordism categories. Adv. Math. 141(1999), 207–281.Google Scholar
[22] Kerler, T., Resolutions of p-Modular TQFT's and Representations of Symmetric Groups. math.GT/0110006.Google Scholar
[23] Kerler, T., The Structure of the Fibonacci TQFT. In preparation.Google Scholar
[24] Kerler, T., p-Modular TQFT's, Milnor-Torsion, and the Casson.Lescop Invariant. Geom. Topol. Monogr. 4(2002), 119–141.Google Scholar
[25] Kerler, T. and Lyubashenko, V. V., Non-semisimple topological quantum field theories for 3-manifolds with corners. Lecture Notes in Math., Springer-Verlag, 2001, to appear.Google Scholar
[26] Kirby, R., A calculus for framed links in S 3 . Invent. Math. 45(1978), 35–56.Google Scholar
[27] Kuperberg, G., Noninvolutory Hopf algebras and 3-manifold invariants. Duke Math. J. (1) 84(1996), 83–129; Involutory Hopf algebras and 3-manifold invariants. Internat. J. Math. (1) 2(1991), 41–66.Google Scholar
[28] Larson, R. G. and Sweedler, M. E., An associative orthogonal bilinear form for Hopf algebras. Amer. J. Math. 91(1969), 75–94.Google Scholar
[29] Lescop, C., Global surgery formula for the Casson–Walker invariant. Ann. of Math. Stud. 140, Princeton University Press, Princeton, NJ, 1996.Google Scholar
[30] Lickorish, W. B. R., An Introduction to Knot Theory. Graduate Texts in Math. 127, Springer Verlag, 1997.Google Scholar
[31] Lyubashenko, V. V., Invariants of 3-manifolds and projective representations of mapping class groups via quantum groups at roots of unity. Comm. Math. Phys. 172(1995), 467–516.Google Scholar
[32] Lyubashenko, V. V. and Majid, S., Braided groups and quantum Fourier transform. J. Algebra (3) 166(1994), 506–528.Google Scholar
[33] Majid, S., Braided groups. J. Pure Appl. Algebra (2) 86(1993), 187–221.Google Scholar
[34] Massey, W. S., A Basic Course in Algebraic Topology. Graduate Texts in Math. 127, Springer Verlag, 1991.Google Scholar
[35] Masbaum, G. and Roberts, J. D., A simple proof of integrality of quantum invariants at prime roots of unity. Math. Proc. Cambridge Philos. Soc. (3) 121(1997), 443–454.Google Scholar
[36] Matveev, S. and Polyak, M., A geometrical presentation of the surface mapping class group and surgery. Comm. Math. Phys. 160(1994), 537–550.Google Scholar
[37] Meng, G. and Taubes, C., Milnor torsion. Math. Res. Lett. (5) 3(1996), 661–674.Google Scholar
[38] Milnor, J., A duality theorem for Reidemeister torsion. Ann. of Math. (2) 76(1962), 137–147.Google Scholar
[39] Murakami, H., Quantum SU(2)-invariants dominate Casson's SU(2)-invariant. Math. Proc. Camb. Phil. Soc. 115(1994), 83–103.Google Scholar
[40] Ohtsuki, T., A polynomial invariant of rational homology 3-spheres. Invent.Math. (2) 123(1996), 241–257.Google Scholar
[41] Radford, D., The Order of the Antipode of a Finite Dimensional Hopf Algebra is Finite. Amer. J. Math. (2) (1976)98, 333–355.Google Scholar
[42] Radford, D., The trace function and Hopf algebras. J. Algebra 163(1994), 583–622.Google Scholar
[43] Reshetikhin, N. Yu. and Turaev, V. G., Invariants of 3-manifolds via link polynomials and quantum groups. Invent.Math. 103(1991), 547–597.Google Scholar
[44] Rozansky, L. and Saleur, H., S- and T-matrices for the super U(1; 1)WZW model. Application to surgery and 3-manifolds invariants based on the Alexander.Conway polynomial. Nuclear Phys. B (2) 389(1993), 365–423.Google Scholar
[45] Turaev, V. G., Reidemeister torsion and the Alexander polynomial. (Russian) Mat. Sb. (N.S.) (2) 18(66)(1976), 252–270.Google Scholar
[46] Turaev, V. G., Quantum invariants of knots and 3-manifolds. de Gruyter Stud. Math. 18, Walter de Gruyter, Berlin, 1994.Google Scholar
[47] Turaev, V. G., A combinatorial formulation for the Seiberg–Witten invariants of 3-manifolds. Math. Res. Lett. (5) 5(1998), 583–598.Google Scholar
[48] Turaev, V. and Viro, O., State sum invariants of 3-manifolds and quantum 6j-symbols. Topology (4) 31(1992), 865–902.Google Scholar
[49] Wajnryb, B., An elementary approach to the mapping class group of a surface. Geom. Topol. 3(1999), 405–466 (electronic); A simple presentation for the mapping class group of an orientable surface. Israel J. Math. 45(1983), 157–174.Google Scholar
[50] Witten, E., Quantum field theory and the Jones polynomial. Comm. Math. Phys. (3) 121(1989), 351–399.Google Scholar
[51] Yetter, D., Portrait of the handle as a Hopf algebra. In: Geometry and physics (Aarhus, 1995), Lecture Notes in Pure and Appl. Math. 184, Dekker, New York, 1997, 481–502.Google Scholar