Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T01:38:51.061Z Has data issue: false hasContentIssue false
  • English
  • Français

The Homotopy of Simplicial Algebras

Published online by Cambridge University Press:  20 November 2018

Harry Lakser
Harry Lakser*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] Walter Taylor investigated the relationship between the algebraic structure of a topological algebra A and the group structure of its fundamental group π1(A) and of the higher homotopy groups πn(A),n > 1. The main result is that a variety 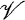satisfies a group law λ in homotopy (that is, π1) if and only if every group in the idempotent reduct of 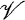obeys λ. (The relevant definitions are in [6] and also § 2 of this paper.) A similar result is stated for the higher homotopy groups. As Taylor points out in the introduction, the hard part of the theorem is constructing a topological algebra in 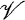whose fundamental group may fail to obey λ; indeed, in [6] this is only done in detail for the commutative law, and the proof is rather computational.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1411 - 1422
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Curtis, E. B., Simplicial homotopy theory, Advances in Mathematics 6 (1971), 107–209.Google Scholar
2. Kan, D. M., On c.s.s. complexes, Amer. J. Math. 79 (1957), 449–476.Google Scholar
3. Lamotke, K., Semisimpliziale algebraische Topologie, Die Grundlehren der mathematischen Wissenschaften, Band 147 (Springer-Verlag, Berlin, Heidelberg, New York, 1968).CrossRefGoogle Scholar
4. Lundell, A. T. and Weingram, S., The topology of CW complexes, University Series in Higher Mathematics (Van Nostrand Reinhold, New York, 1969).CrossRefGoogle Scholar
5. May, J. P., Simplicial objects in algebraic topology, Van Nostrand Mathematical Studies #11 (D. Van Nostrand, Princeton, N.J., 1967).Google Scholar
6. Taylor, Walter, Varieties obeying homotopy laws, Can. J. Math. 29 (1977), 498–527 Google Scholar