Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T05:35:19.325Z Has data issue: false hasContentIssue false
  • English
  • Français

The Homotopy Set of the Axes of Pairings

Published online by Cambridge University Press:  20 November 2018

Nobuyuki Oda
Nobuyuki Oda*
Affiliation:
Department of Applied Mathematics, Faculty of Science, Fukuoka University, 8-19-1, Nanakuma, Jonanku, Fukuoka 814-01, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

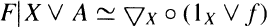Varadarajan [13] named a map f: A → X a cyclic map when there exists a map F: X × A → X such that for the folding map ∇X: X ∨ X → X. He defined the generalized Gottlieb set G(A, X) of the homotopy classes of the cyclic maps F: A → X and studied the fundamental properties of G(A, X) If A is a co-Hopf space, then the Varadarajan set G(A, X) has a group structure [13]. The group G(A,X) is a generalization of G(X) and Gn(X) of Gottlieb [2,3]. Some authors studied the properties of the Varadarajan set, its dual and related topics [4, 5, 6, 7,12,15,16,17].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 5 , 01 October 1990 , pp. 856 - 868
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Arkowitz, M. The generalized Whitehead product Pacific J. Math. 12 (1962) 7–23.Google Scholar
2. Gottlieb, D.H. A certain subgroup of the fundamental group Amer. J. Math. 87 (1965) 840–856.Google Scholar
3. Gottlieb, D.H. Evaluation subgroups of homotopy groups Amer. J. Math. 91 (1969) 729–756.Google Scholar
4. Hoo, C.S. Cyclic maps from suspensions to suspensions Canad. J. Math. 24 (1972) 789–791.Google Scholar
5. Lim, K.L. On cyclic maps J. Austral. Math. Soc. Ser. A32 (1982) 349–357.Google Scholar
6. Lim, K.L. On evaluation subgroups of generalized homotopy groups Canad. Math. Bull. 27 (1984) 78–86.Google Scholar
7. Lim, K.L. Cocyclic maps and coevaluation subgroups Canad. Math. Bull. 30 (1987) 63–71.Google Scholar
8. Murayama, M. On G-ANR's and their G-homotopy types Osaka J. Math. 20 (1983) 479–512.Google Scholar
9. Matumoto, T. Equivariant cohomology theories on G-CW complexes Osaka J. Math. 10 (1973) 51–68.Google Scholar
10. Matumoto, T. A complement to the theory of G-CW complexes Japan. J. Math. 10 (1984) 353–374.Google Scholar
11. Oda, N. Pairings and copairings in the category of topological spaces preprintGoogle Scholar
12. Siegel, J. G-spaces, H-spaces and W-spaces Pacific J. Math. 31 (1969) 209–214.Google Scholar
13. Varadarajan, K. Generalized Gottlieb groups J. Indian Math. Soc. 33 (1969) 141–164.Google Scholar
14. Whitehead, G.W. Elements of homotopy theory Graduate texts in Math. 61, SpringerVerlag (1978).Google Scholar
15. Woo, M.H. and Kim, J.R. Certain subgroups of homotopy groups J. Korean Math. Soc. 21 (1984) 109–120.Google Scholar
16. Woo, M.H. and Lee, K.Y. The relative evaluation subgroups of a CW-pair J. Korean Math. Soc. 25 (1988) 149–160.Google Scholar