Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T14:05:08.745Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolic Group C*-Algebras and Free-Product C*-Algebras as Compact Quantum Metric Spaces

Published online by Cambridge University Press:  20 November 2018

Narutaka Ozawa  and
Marc A. Rieffel
Narutaka Ozawa
Affiliation:
Department of Mathematical Science, University of Tokyo, Komaba, 153-8914, Japan, e-mail: narutaka@ms.u-tokyo.ac.jp
Marc A. Rieffel
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, U.S.A., e-mail: rieffel@math.berkeley.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

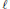Let $\ell $ be a length function on a group 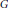$G$, and let 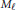${{M}_{\ell }}$ denote the operator of pointwise multiplication by 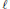$\ell $ on 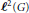${{\ell }^{2}}\left( G \right)$. Following Connes, 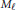${{M}_{\ell }}$ can be used as a “Dirac” operator for 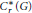$C_{r}^{*}\left( G \right)$. It defines a Lipschitz seminorm on 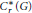$C_{r}^{*}\left( G \right)$, which defines a metric on the state space of 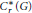$C_{r}^{*}\left( G \right)$. We show that if 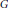$G$ is a hyperbolic group and if 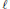$\ell $ is a word-length function on 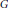$G$, then the topology from this metric coincides with the weak-$*$ topology (our definition of a “compact quantum metric space”). We show that a convenient framework is that of filtered 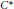${{C}^{*}}$-algebras which satisfy a suitable “Haagerup-type” condition. We also use this framework to prove an analogous fact for certain reduced free products of 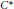${{C}^{*}}$-algebras.

Keywords

Primary: 46L87secondary: 20F6746L09
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 5 , 01 October 2005 , pp. 1056 - 1079
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Antonescu, C. and Christensen, E., Metrics on group C*-algebras and a non-commutative Arzelà-Ascoli theorem. J Funct. Anal. 214(2004), 247–259. arXiv:math.OA/0211312.Google Scholar
[2] Avitzour, D., Free products of C*-algebras. Trans. Amer. Math. Soc. 271(1982), 423–465.Google Scholar
[3] Bucher, M. and Karlsson, A., On the definition of bolic spaces. Expo. Math. 20(2002), 269–277.Google Scholar
[4] Connes, A., Compact metric spaces, Fredholm modules, and hyperfiniteness. Ergodic Theory Dynam. Systems 9(1989), 207–220.Google Scholar
[5] Connes, A., Noncommutative Geometry. Academic Press, San Diego, CA, 1994.Google Scholar
[6] Dykema, K., Haagerup, U., and Rørdam, M., The stable rank of some free product C*-algebras. Duke Math. J. 90(1997), 95–121. Correction: Duke Math. J. 94(1998), 213.Google Scholar
[7] Figà-Talamanca, A., Harmonic Analysis on Free Groups. Lecture Notes in Pure and Applied Mathematics 87, Marcel Dekker, New York, 1983.Google Scholar
[8] É. Ghys and de la Harpe, P., editors, Sur les groupes hyperboliques d’après Mikhael Gromov. Progress in Mathematics 83, Birkhäuser, Boston, MA, 1990.Google Scholar
[9] Haagerup, U., An example of a non nuclear C*-algebra which has the metric approximation property. Invent.Math. 50(1978/79), 279–293.Google Scholar
[10] Jolissaint, P., Rapidly decreasing functions in reduced C*-algebras of groups. Trans. Amer.Math. Soc. 317(1990), 167–196.Google Scholar
[11] Kasparov, G. and Skandalis, G., Groupes “boliques” et conjecture de Novikov. C. R. Acad. Sci. Paris Sér. I Math. 319(1994), 815–820.Google Scholar
[12] Rieffel, M. A., Metrics on states from actions of compact groups. Doc. Math. 3(1998), 215–229. arXiv:math.OA/9807084.Google Scholar
[13] Rieffel, M. A., Metrics on state spaces. Doc. Math. 4(1999), 559–600. arXiv:math.OA/9906151.Google Scholar
[14] Rieffel, M. A., Gromov-Hausdorff Distance for Quantum Metric Spaces. Mem. Amer.Math. Soc. 168, no. 796, 2004, 1–65. arXiv:math.04/0011063.Google Scholar
[15] Rieffel, M. A., Group C*-algebras as compact quantum metric spaces. Doc. Math. 7(2002), 605–651. arXiv:math.OA/0205195.Google Scholar
[16] Voiculescu, D., Symmetries of some reduced free product C*-algebras. In: Operator Algebras and their Connections with Topology and Ergodic Theory, Lecture Notes in Math. 1132, Springer-Verlag, Berlin, 1985, pp. 556–588.Google Scholar
[17] Voiculescu, D., On the existence of quasicentral approximate units relative to normed ideals. I. J. Funct. Anal. 91(1990), 1–36.Google Scholar
[18] Voiculescu, D. V., Dykema, K. J., and Nica, A., Free Random Variables. CRM Monograph Series 1, American Mathematical Society, Providence, RI, 1992.Google Scholar