Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T05:04:37.649Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideal Structure of Multiplier Algebras of Simple C*-algebras With Real Rank Zero

Published online by Cambridge University Press:  20 November 2018

Francesc Perera
Francesc Perera*
Affiliation:
Departament de Matemàtiques Universitat Autònoma de Barcelona 08193 Bellaterra, Barcelona Spain, e-mail: perera@mat.uab.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a description of the monoid of Murray-von Neumann equivalence classes of projections for multiplier algebras of a wide class of 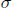$\sigma $-unital simple 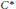${{C}^{*}}$-algebras 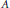$A$ with real rank zero and stable rank one. The lattice of ideals of this monoid, which is known to be crucial for understanding the ideal structure of the multiplier algebra 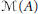$\mathcal{M}(A)$, is therefore analyzed. In important cases it is shown that, if 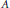$A$ has finite scale then the quotient of 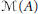$\mathcal{M}(A)$ modulo any closed ideal 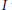$I$ that properly contains 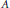$A$ has stable rank one. The intricacy of the ideal structure of 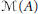$\mathcal{M}(A)$ is reflected in the fact that 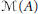$\mathcal{M}(A)$ can have uncountably many different quotients, each one having uncountably many closed ideals forming a chain with respect to inclusion.

Keywords

46L0546L8006F05C*-algebramultiplier algebrareal rank zerostable rankrefinement monoid
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 3 , 01 June 2001 , pp. 592 - 630
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Alfsen, E. M., Compact convex sets and boundary integrals. Ergebnisse der Math. und ihre Grenzgebiete, Band 57, Springer-Verlag, Berlin, 1971.Google Scholar
[2] Ara, P. and Pardo, E., Refinement monoids with weak comparability and applications to regular rings and C*-algebras. Proc. Amer. Math. Soc. (3) 124 (1996), 715–720.Google Scholar
[3] Ara, P., Goodearl, K. R., O’Meara, K. C. and Pardo, E., Separative cancellation for projective modules over exchange rings. Israel J. Math. 105 (1998), 105–137.Google Scholar
[4] Blackadar, B., Traces on simple AF C*-algebras. J. Funct. Anal. 38 (1980), 156–168.Google Scholar
[5] Blackadar, B., Comparison theory for simple C*-algebras. In: Operator Algebras and Applications (eds., D. Evans and M. Takesaki), LondonMath. Soc. Lecture Notes 135, 1988, 21–54.Google Scholar
[6] Blackadar, B., Rational C*-algebras and non-stable K-Theory. Rocky Mountain J. Math. 20 (1990), 285–316.Google Scholar
[7] Blackadar, B., K-Theory for Operator Algebras. MSRI Pub. 5 (Second Edition), Cambridge University Press, 1998.Google Scholar
[8] Blackadar, B. and Handelman, D., Dimension functions and traces on C*-algebras. J. Funct. Anal. 45 (1982), 297–340.Google Scholar
[9] Blackadar, B. and Rørdam, M., Extending states on preordered semigroups and the existence of quasitraces on C*-algebras. J. Algebra 152 (1992), 240–247.Google Scholar
[10] Brown, L. G., Semicontinuity and multipliers of C*-algebras. Canad. J. Math. 40 (1988), 865–988.Google Scholar
[11] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99 (1991), 131–149.Google Scholar
[12] Brown, L. G. and Pedersen, G. K., On the geometry of the unit ball of a C*-algebra. J. Reine Angew.Math. 469 (1995), 113–147.Google Scholar
[13] Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups, Vol. 1. Math. Surveys, 7, Amer. Math. Soc., Providence, 1961.Google Scholar
[14] Cuntz, J., The structure of multiplication and addition on simple C*-algebras. Math. Scand. 40 (1977), 215–233.Google Scholar
[15] Cuntz, J., Dimension functions on simple C*-algebras. Math. Ann. 233 (1978), 181–197.Google Scholar
[16] Cuntz, J., K-Theory for certain C*-algebras. Ann. of Math. 113 (1981), 181–197.Google Scholar
[17] Cuntz, J. and Pedersen, G. K., Equivalence and traces on C*-algebras. J. Funct. Anal. 33 (1979), 135–164.Google Scholar
[18] Dobbertin, H., Refinement monoids, Vaught monoids, and Boolean algebras. Math. Ann. 265 (1983), 473–487.Google Scholar
[19] Effros, E. G., Handelman, D. E. and Shen, C.-L., Dimension groups and their affine representations. Amer. J. Math. 102 (1980), 385–407.Google Scholar
[20] Elliott, G. A., Derivations of matroid C*-algebras II. Ann. of Math. 100 (1974), 407–422.Google Scholar
[21] Elliott, G. A., On the classification of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 38 (1976), 29–44.Google Scholar
[22] Elliott, G. A., The ideal structure of the multiplier algebra of an AF algebra. C. R. Math. Rep. Acad. Sci. Canada 9 (1987), 225–230.Google Scholar
[23] Elliott, G. A., Dimension groups with torsion. Internat. J. Math. 1 (1990), 361–380.Google Scholar
[24] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew.Math. 443 (1993), 179–219.Google Scholar
[25] Engelking, R., General topology. Rev. and Compl. Ed., Heldermann Verlag, Berlin, 1989.Google Scholar
[26] Goodearl, K. R., Partially ordered abelian groups with interpolation. Math. Surveys and Monographs, 20, Amer.Math. Soc., Providence, 1986.Google Scholar
[27] Goodearl, K. R., Extensions of dimension groups and AF C*-algebras. J. Reine Angew.Math. 412 (1990), 150–219.Google Scholar
[28] Goodearl, K. R., Notes on a class of simpleC*-algebras with real rank zero. Publ.Matem. 36 (1992), 637–654.Google Scholar
[29] Goodearl, K. R., Riesz decomposition in inductive limit C*-algebras. Rocky Mountain J. Math. (4) 24 (1994), 1405–1430.Google Scholar
[30] Goodearl, K. R., K0 of multiplier algebras of C*-algebras with real rank zero. K-Theory 10 (1996), 419–489.Google Scholar
[31] Goodearl, K. R. and Handelman, D. E., Stenosis in dimension groups and AF C*-algebras. J. Reine Angew.Math. 332 (1982), 1–98.Google Scholar
[32] Handelman, D. E., Homomorphisms of C*-algebras to finite AW*-algebras. Michigan Math. J. 28 (1981), 229–240.Google Scholar
[33] Larsen, N. and Osaka, H., Extremal richness of multiplier algebras of corona algebras of simple C*-algebras. J.Operator Theory 38 (1997), 131–149.Google Scholar
[34] Lin, H., Ideals of multiplier algebras of simple AF C*-algebras. Proc. Amer.Math. Soc. 104 (1988), 239–244.Google Scholar
[35] Lin, H., Simple C*-algebras with continuous scales and simple corona algebras. Proc. Amer. Math. Soc. (3) 112 (1991), 871–880.Google Scholar
[36] Lin, H., Notes on K-Theory ofmultiplier algebras and corona algebras. preprint.Google Scholar
[37] Lin, H., Exponential rank of C*-algebras with real rank zero and the Brown-Pedersen conjectures. J. Funct. Anal. 114 (1993), 1–11.Google Scholar
[38] Lin, H., Extensions by C*-algebras of real rank zero, III. Proc. LondonMath. Soc. (3) 76 (1998), 634–666.Google Scholar
[39] Lin, H. and Zhang, S., On infinite simple C*-algebras. J. Funct. Anal. 100 (1991), 221–231.Google Scholar
[40] Lin, H. and Zhang, S., Certain simple C*-algebras with nonzero real rank whose corona algebras have real rank zero. Houston J. Math. (1) 18 (1992), 57–71.Google Scholar
[41] Pardo, E., Metric completions of ordered groups and K0 of exchange rings. Trans. Amer.Math. Soc. (3) 350 (1998), 913–933.Google Scholar
[42] Pedersen, G. K., C*-algebras and their automorphism groups. Academic Press, London, New York, 1979.Google Scholar
[43] Perera, F., The structure of positive elements for C*-algebras with real rank zero. Internat. J. Math. (3) 8 (1997), 383–405.Google Scholar
[44] Perera, F., Extremal richness of multiplier and corona algebras of simple C*-algebras with real rank zero. J. Operator Theory 44 (2000), 413–431.Google Scholar
[45] Rieffel, M. A., Dimension and stable rank in the K-Theory of C*-algebras. Proc. LondonMath. Soc. (3) 46 (1983), 301–333.Google Scholar
[46] Rørdam, M., Advances in the theory of unitary rank and countable approximation. Ann. of Math. 128 (1988), 153–172.Google Scholar
[47] Rørdam, M., Ideals in the multiplier algebra of a stable C*-algebra. J. Operator Theory 25 (1991), 283–298.Google Scholar
[48] Rørdam, M., On the structure of simple C*-algebras tensored with a UHF-algebra. II, J. Funct. Anal. 107 (1992), 255–269.Google Scholar
[49] Rørdam, M., On sums of finite projections. Operator algebras and operator theory, Shanghai, 1997, 327–340, Contemporary Math. 228, Amer.Math. Soc., Providence, RI, 1998.Google Scholar
[50] Villadsen, J., Simple C*-algebras with perforation. J. Funct. Anal. (1) 154 (1998), 110–116.Google Scholar
[51] Warfield, R. B., Exchange rings and decomposition of modules. Math. Ann. 199 (1972), 31–36.Google Scholar
[52] Wehrung, F., Injective positively ordered monoids, I, II. J. Pure Applied Algebra 83 (1992), 43–82, 83–100.Google Scholar
[53] Wehrung, F., Monoids of intervals of ordered abelian groups. J. Algebra 182 (1996), 287–328.Google Scholar
[54] Zhang, S., On the structure of projections and ideals of corona algebras. Canad. J. Math. 41 (1989), 721–742.Google Scholar
[55] Zhang, S., C*-algebras with real rank zero and the internal structure of their corona and multiplier algebras, Part III. Canad. J. Math. 42 (1990), 159–190.Google Scholar
[56] Zhang, S., A Riesz decomposition property and ideal structure of multiplier algebras. J. Operator Theory 24 (1990), 209–225.Google Scholar
[57] Zhang, S., K1-groups, quasidiagonality, and interpolation by multiplier projections. Trans. Amer.Math. Soc. 325 (1991), 793–818.Google Scholar
[58] Zhang, S., C*-algebras with real rank zero and their corona and multiplier algebras, Part I. Pacific J. Math. 155 (1992), 169–197.Google Scholar
[59] Zhang, S., C*-algebras with real rank zero and their corona and multiplier algebras, Part II. K-Theory 6 (1992), 1–27.Google Scholar
[60] Zhang, S., C*-algebras with real rank zero and their corona and multiplier algebras, Part IV. Internat. J. Math. 3 (1992), 309–336.Google Scholar