Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T20:16:33.883Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideas from Zariski Topology in the Study of Cubical Homology

Published online by Cambridge University Press:  20 November 2018

Tomasz Kaczynski ,
Marian Mrozek  and
Anik Trahan
Tomasz Kaczynski
Affiliation:
Département de Mathématiques, Université de Sherbrooke, Sherbrooke, QC, J1K 2R1 email: Tomasz.Kaczynski@usherbrooke.ca, Anik.Trahan@usherbrooke.ca
Marian Mrozek
Affiliation:
Division of Computational Mathematics, Graduate School of Business, ul. Zielona 27, 33-300 Nowy Sącz, Poland, email: Marian.Mrozek@wsb-nlu.edu.pl and Institute of Computer Science, Jagiellonian University, 31-072 Kraków, PolandMarian.Mrozek@ii.uj.edu.pl
Anik Trahan
Affiliation:
Département de Mathématiques, Université de Sherbrooke, Sherbrooke, QC, J1K 2R1 email: Tomasz.Kaczynski@usherbrooke.ca, Anik.Trahan@usherbrooke.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Cubical sets and their homology have been used in dynamical systems as well as in digital imaging. We take a fresh look at this topic, following Zariski ideas from algebraic geometry. The cubical topology is defined to be a topology in 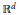${{\mathbb{R}}^{d}}$ in which a set is closed if and only if it is cubical. This concept is a convenient frame for describing a variety of important features of cubical sets. Separation axioms which, in general, are not satisfied here, characterize exactly those pairs of points which we want to distinguish. The noetherian property guarantees the correctness of the algorithms. Moreover, maps between cubical sets which are continuous and closed with respect to the cubical topology are precisely those for whom the homology map can be defined and computed without grid subdivisions. A combinatorial version of the Vietoris–Begle theorem is derived. This theorem plays the central role in an algorithm computing homology of maps which are continuous with respect to the Euclidean topology.

Keywords

55–0452B0554C6068W0568W3068U10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 5 , 01 October 2007 , pp. 1008 - 1028
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Allili, M. and Kaczynski, T., An algorithmic approach to the construction of homomorphisms induced by maps in homology. Trans. Amer. Math. Soc. 352(2000), no. 5, 2261–2281.Google Scholar
[2] Allili, M., Mischaikow, K., and Tannenbaum, A., Cubical homology and the topological classification of 2D and 3D imagery. ICIP-01, 2(2001), 173–176.Google Scholar
[3] Allili, M. and Ziou, D., Topological feature extraction in binary images. In: Proc. 6th Intl. Symposium on Signal Processing and its Appl., Vol. 2, IEEE 2001, 651–654.Google Scholar
[4] Dieudonné, J. A., Cours de géométrie algébrique, Collection SUP, Le mathématicien, 10-11, Paris 1974.Google Scholar
[5] Dieudonné, J. A., History of Algebraic and Differential Topology, Springer, 1989.Google Scholar
[6] Ehrenborg, R. and Hetyei, G., Generalizations of Baxter's theorem and cubical homology. J. Combin. Theory, Ser. A 69(1995), no. 2, 233–287.Google Scholar
[7] Górniewicz, L., Homological Methods in Fixed Point Theory of Multi-Valued Maps. Dissertationes Math. 129, PWN, Warsaw, 1976.Google Scholar
[8] Jacobson, N., Basic Algebra. II. W. H. Freedman, San Francisco, 1974,Google Scholar
[9] Kaczynski, T., Mischaikow, K., and Mrozek, M., Computational Homology. Applied Mathematical Sciences 157, Springer-Verlag, New York, 2004.Google Scholar
[10] Massey, W. S., A Basic Course in Algebraic Topology. Graduate Texts in Mathematics 127, Springer-Verlag, New York, 1991.Google Scholar
[11] Mischaikow, K., Mrozek, M., and Pilarczyk, P., Graph approach to the computation of the homology of continuous maps. Found. Comput. Math. 5(2005), no. 2, 199–229.Google Scholar
[12] Moore, R. E., Interval Analysis. Prentice-Hall, Englewood Cliffs, NJ, 1966.Google Scholar
[13] Mrozek, M., An algorithm approach to the Conley index theory. J. Dynam. Differential Equations 11(1999), no. 4, 711–734.Google Scholar
[14] Mrozek, M., Topological invariants, multivalued maps and computer assisted proofs in dynamics. Comput. Math. Appl. 32(1996), no. 4, 83–104.Google Scholar
[15] Mrozek, M. and Zgliczyński, P., Set arithmetic and the enclosing problem in dynamics, Ann. Polon. Math. 74(2000), 237–259.Google Scholar
[16] Szymczak, A., A combinatorial procedure for finding isolating neighbourhoods and index pairs. Proc. Roy. Soc. Edinburgh Sect. A 127(1997), no. 5, 1075–1088.Google Scholar
[17] Szymczak, A., Index Pairs: From Dynamics to Combinatorics and Back. Ph.D. thesis, Georgia Institute of Technology, Atlanta, 1999.Google Scholar
[18] Trahan, A., Ensembles cubiques: Topologie et algorithmes de correction d’homologie. M.Sc. dissertation, Université de Sherbrooke, Sherbrooke, QC, 2004.Google Scholar