Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bennett, G
1973.
Inclusion mappings between lp spaces.
Journal of Functional Analysis,
Vol. 13,
Issue. 1,
p.
20.
Batt, J�rgen
Dierolf, Peter
and
Voigt, J�rgen
1977.
Summable sequences and topological properties ofm 0(I).
Archiv der Mathematik,
Vol. 28,
Issue. 1,
p.
86.
Stieglitz, Michael
and
Tietz, Hubert
1977.
Matrixtransformationen von Folgenr�umen Eine Ergebnis�bersicht.
Mathematische Zeitschrift,
Vol. 154,
Issue. 1,
p.
1.
Devos, Robert
1978.
Category of sequences of zeros and ones in some FK spaces.
Glasgow Mathematical Journal,
Vol. 19,
Issue. 2,
p.
121.
Swetits, J.
1978.
A characterization of a class of barrelled sequence spaces.
Glasgow Mathematical Journal,
Vol. 19,
Issue. 1,
p.
27.
Turpin, Philippe
1978.
Vector Space Measures and Applications II.
Vol. 645,
Issue. ,
p.
180.
Saxon, Stephen A.
and
Narayanaswami, P.P.
1981.
Metrizable (LF)-spaces, (db)-spaces, and the separable quotient problem.
Bulletin of the Australian Mathematical Society,
Vol. 23,
Issue. 1,
p.
65.
Schaffer, Matthew
and
Snyder, A. K.
1986.
Properties of sequence spaces in whichl 1 is weakly compactly embedded.
Mathematische Zeitschrift,
Vol. 192,
Issue. 4,
p.
569.
Narayanaswami, P.P.
1986.
Complex Analysis, Functional Analysis and Approximation Theory, Proceedings of the Conference on Complex Analysis and Approximation Theory Universidade Estadual de Campinas.
Vol. 125,
Issue. ,
p.
247.
Snyder, A. K.
1986.
A property of the embedding of 𝑐₀ in 𝑙_{∞}.
Proceedings of the American Mathematical Society,
Vol. 97,
Issue. 1,
p.
59.
1987.
Barrelled Locally Convex Spaces.
Vol. 131,
Issue. ,
p.
484.
Stadler, Wolfgang
1987.
Zu einer Frage von Wilansky.
Archiv der Mathematik,
Vol. 48,
Issue. 2,
p.
149.
Bennett, Grahame
1987.
Sequence spaces with small ?-duals.
Mathematische Zeitschrift,
Vol. 194,
Issue. 3,
p.
321.
Connor, J.
and
Loomis, I.
1989.
Isometries on conservative subalgebras of bounded sequences.
Proceedings of the American Mathematical Society,
Vol. 107,
Issue. 3,
p.
743.
Grosse-Erdmann, Karl-Goswin
1992.
Matrix transformations involving analytic sequence spaces.
Mathematische Zeitschrift,
Vol. 209,
Issue. 1,
p.
499.
Grosse-Erdmann, Karl-Goswin
1993.
T-Solid Sequence Spaces.
Results in Mathematics,
Vol. 23,
Issue. 3-4,
p.
302.
Sarıgöl, Mehmet Ali
1993.
On two absolute Riesz summability factors of infinite series.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 2,
p.
485.
Narayanaswami, P. P.
1993.
Functional Analysis and Related Topics, 1991.
Vol. 1540,
Issue. ,
p.
289.
Drewnowski, Lech
Florencio, Miguel
and
Paúl, Pedro J.
1994.
Barrelled subspaces of spaces with subseries decompositions or Boolean rings of projections.
Glasgow Mathematical Journal,
Vol. 36,
Issue. 1,
p.
57.
Stuart, Christopher E.
1996.
Weak Sequential Completeness of $\b$-Duals.
Rocky Mountain Journal of Mathematics,
Vol. 26,
Issue. 4,


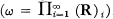 . A K-space
. A K-space 