Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-27T17:02:50.936Z Has data issue: false hasContentIssue false
  • English
  • Français

The Index of an Extremal Arc

Published online by Cambridge University Press:  20 November 2018

William Karush
William Karush*
Affiliation:
The University of Chicago
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We are concerned with extremal arcs for the problem of minimizing a function

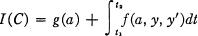
over a class of parametric curves C in ay-space of the form

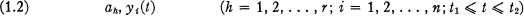
and satisfying end conditions of the type

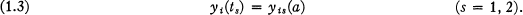
The components ah are constants and the functions g, yis, and/are given, with the last function positively homogeneous of degree one.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 4 , 1952 , pp. 281 - 294
Copyright
Copyright © Canadian Mathematical Society 1952

References

1. Birkhoff, G. D. and Hestenes, M. R., Natural isoperimetric conditions in the calculus of variations, Duke Math. J., vol. 1 (1935), 198–286.Google Scholar
2. Hazard, K. E., Index theorems for the problem of Bolza, Contributions to the Calculus of Variations, 1938-41 (Chicago).Google Scholar
3. Hestenes, M. R., A theory of critical points, Amer. J. Math., vol. 67 (1945), 521–562.Google Scholar
4. Karush, W., Isoperimetric problems in the calculus of variations, Can. J. Math., vol. 4 (1952), 257–280.Google Scholar
5. Morse, M., The calculus of variations in the large (American Mathematical Society, Colloquium Publications, vol. 18, 1934).Google Scholar
6. Morse, M., A special parameterization of curves, Bull. Amer. Math. Soc, vol. 42 (1936), 915–922.Google Scholar
7. Morse, M., Functional topology and abstract variational theory, Ann. Math., vol. 38 (1937), 386–449.Google Scholar