Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T12:56:59.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitely Divisible Laws Associated with Hyperbolic Functions

Published online by Cambridge University Press:  20 November 2018

Jim Pitman  and
Marc Yor
Jim Pitman
Affiliation:
Department of Statistics, University of California, 367 Evans Hall # 3860, Berkeley, CA 94720-3860, USA
Marc Yor
Affiliation:
Laboratoire de Probabilités, case 188, Université Pierre et Marie Curie, 4, place Jussieu, F-75252 Paris Cedex 05, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The infinitely divisible distributions on 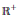${{\mathbb{R}}^{+}}$ of random variables 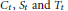${{C}_{t}},\,{{S}_{t}}\,\text{and}\,{{T}_{t}}$ with Laplace transforms

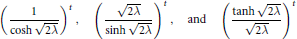$${{\left( \frac{1}{\cosh \sqrt{2\lambda }} \right)}^{t}},{{\left( \frac{\sqrt{2\lambda }}{\sinh \sqrt{2\lambda }} \right)}^{t}},\,\text{and}\,{{\left( \frac{\tanh \sqrt{2\lambda }}{\sqrt{2\lambda }} \right)}^{t}}$$

respectively are characterized for various $t\,>\,0$ in a number of different ways: by simple relations between their moments and cumulants, by corresponding relations between the distributions and their Lévy measures, by recursions for their Mellin transforms, and by differential equations satisfied by their Laplace transforms. Some of these results are interpreted probabilistically via known appearances of these distributions for 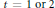$t\,=\,1\,\,\text{or}\,2$ in the description of the laws of various functionals of Brownian motion and Bessel processes, such as the heights and lengths of excursions of a one-dimensional Brownian motion. The distributions of 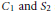${{C}_{1}}\,\text{and}\,{{S}_{2}}$ are also known to appear in the Mellin representations of two important functions in analytic number theory, the Riemann zeta function and the Dirichlet 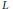$L$-function associated with the quadratic character modulo 4. Related families of infinitely divisible laws, including the gamma, logistic and generalized hyperbolic secant distributions, are derived from 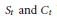${{S}_{t}}\,\text{and}\,{{C}_{t}}$ by operations such as Brownian subordination, exponential tilting, and weak limits, and characterized in various ways.

Keywords

11M0660J6560E07Riemann zeta functionMellin transformcharacterization of distributionsBrownian motionBessel processLévy processgamma processMeixner process
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 2 , 01 April 2003 , pp. 292 - 330
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Aldous, D. J., The continuum random tree II: an overview. In: Stochastic Analysis (eds. M. T. Barlow and N. H. Bingham), Cambridge University Press, 1991, 23–70.Google Scholar
[2] Aldous, D. J., The ζ(2) limit in the random assignment problem. Random Structures Algorithms 18 (2001), 381–418.Google Scholar
[3] Andrews, G. E., Askey, R., and Roy, R., Special Functions. Encyclopedia of Math. and Appl. Vol. 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[4] Arratia, R. and Goldstein, L., Size biasing: when is the increment independent. Preprint, 1998.Google Scholar
[5] Barndorff-Nielsen, O., Kent, J. and Sørensen, M., Normal variance-mean mixtures and z distributions. Internat. Statist. Rev. 50 (1982), 145–159.Google Scholar
[6] Bertoin, J., Lévy processes. Cambridge University Press, Cambridge, 1996.Google Scholar
[7] Biane, P., Comparaison entre temps d'atteinte et temps de séjour de certaines diffusions réelles. In: Séminaire de Probabilités XIX, Springer Lecture Notes in Math. 1123 (1985), 291–296.Google Scholar
[8] Biane, P., Pitman, J. and Yor, M., Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions. Bull. Amer.Math. Soc. 38 (2001), 435–465.Google Scholar
[9] Biane, P. and Yor, M., Valeurs principales associées aux temps locaux Browniens. Bull. Sci. Math. (2) 111 (1987), 23–101.Google Scholar
[10] Billingsley, P., Probability and Measure. 3rd edition, Wiley, New York, 1995.Google Scholar
[11] Blumenthal, R. M., Excursions of Markov processes. Birkhäuser, 1992.Google Scholar
[12] Borodin, A. N. and Salminen, P., Handbook of Brownian motion.facts and formulae. Birkhäuser, 1996; second edition, 2002.Google Scholar
[13] Cameron, R. H. and Martin, W. T., Transformation of Wiener integrals under a general class of linear transformations. Trans. Amer.Math. Soc. 58 (1945), 184–219.Google Scholar
[14] Carlitz, L., Bernoulli and Euler numbers and orthogonal polynomials. Duke Math. J 26 (1959), 1–15.Google Scholar
[15] Chung, K. L., Excursions in Brownian motion. Ark. Mat. 14 (1976), 155–177.Google Scholar
[16] Chung, K. L., A cluster of great formulas. Acta Math. Hungar. 39 (1982), 65–67.Google Scholar
[17] Ciesielski, Z. and Taylor, S. J., First passage times and sojourn density for Brownian motion in space and the exact Hausdorff measure of the sample path. Trans. Amer.Math. Soc. 103 (1962), 434–450.Google Scholar
[18] Comtet, A., Monthus, C. and Yor, M., Exponential functionals of Brownian motion and disordered systems. J. Appl. Probab. (2) 35 (1998), 255–271.Google Scholar
[19] Comtet, L., Advanced Combinatorics. D. Reidel Pub. Co., Boston, 1974 (transl. from French).Google Scholar
[20] Di Bucchianico, A., Probabilistic and analytical aspects of the umbral calculus. Stichting Mathematisch Centrum, Centrum voor Wiskunde en Informatica, Amsterdam, 1997.Google Scholar
[21] Dilcher, K., Skula, L. and Slavutskiĭ, I. Sh., Bernoulli numbers. Bibliography (1713–1990). Queen's Papers in Pure and Appl. Math. 87, Queen's University, Kingston, ON, 1991.Google Scholar
[22] Erdélyi, A. et al., Higher Transcendental Functions. Vol. I. Bateman Manuscript Project, McGraw-Hill, New York, 1953.Google Scholar
[23] Erdélyi, A., Tables of Integral Transforms. Vol. I. Bateman Manuscript Project, McGraw-Hill, New York, 1954.Google Scholar
[24] Feinsilver, P., Special Functions, Probability Semigroups, and Hamiltonian Flows. Lecture Notes in Math. 696, Springer, New York, 1978.Google Scholar
[25] Feinsilver, P. and Schott, R., Algebraic structures and operator calculus. Vol. I. Kluwer Academic Publishers Group, Dordrecht, 1993.Google Scholar
[26] Feller, W., An Introduction to Probability Theory and its Applications. Vol. 2. 2nd edition, Wiley, New York, 1971.Google Scholar
[27] Fitzsimmons, P. J. and Getoor, R. K., On the distribution of the Hilbert transform of the local time of a symmetric Lévy process. Ann. Probab. (3) 20 (1992), 1484–1497.Google Scholar
[28] Flajolet, P. and Louchard, G., Analytic variations on the Airy distribution. Algorithmica (3) 31 (2001), 361–377.Google Scholar
[29] Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous elliptiques sur certains groupes nilpotents. Acta Math. (1–2) 139 (1977), 95–153.Google Scholar
[30] Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series and Products. Corrected and enlarged edition, Academic Press, New York, 1980.Google Scholar
[31] Grigelionis, B., Processes of Meixner type. Liet. Matem. Rink. 39 (1999), 40–51.Google Scholar
[32] Grigelionis, B., Generalized z-distributions and related stochastic processes. Technical Report 2000-22, Institute of Mathematics and Informatics, Vilnius, Lithuania, 2000.Google Scholar
[33] Hald, A., The early history of the cumulants and the Gram-Charlier series. Internat. Statist. Rev. 68 (2000), 137–153.Google Scholar
[34] Harkness, W. L. and Harkness, M. L., Generalized hyperbolic secant distributions. J. Amer. Statist. Assoc. 63 (1968), 329–337.Google Scholar
[35] Ikeda, N. and Watanabe, S., Stochastic Differential Equations and Diffusion Processes. 2nd edition, North Holland/Kodansha, 1989.Google Scholar
[36] Itô, K., Poisson point processes attached to Markov processes. In: Proc. 6th Berkeley Sympos. Math. Stat. Prob. Vol. 3, University of California Press, Berkeley, CA, 1972.Google Scholar
[37] Itô, K. and McKean, H. P., Diffusion Processes and their Sample Paths. Springer, 1965.Google Scholar
[38] Kamke, E., Differentialgleichungen. Lçsungsmethoden und Lçsungen. Band I. Gewçhnliche Differentialgleichungen. 3rd edition, Chelsea Publishing Co., New York, 1959.Google Scholar
[39] Knight, F. B., Random walks and a sojourn density process of Brownian motion. Trans. Amer. Math. Soc. 107 (1963), 36–56.Google Scholar
[40] Knight, F. B., Brownian local times and taboo processes. Trans. Amer.Math. Soc. 143 (1969), 173–185.Google Scholar
[41] Kotz, S. and Johnson, N. L. (eds.), Logistic Distribution. Encyclopedia of Statistical Sciences Vol. 5, Wiley, 1985, 123–128.Google Scholar
[42] Lai, T. L., Martingales and boundary crossing probabilities for Markov processes. Ann. Probab. 2 (1974), 1152–1167.Google Scholar
[43] Lévy, P., Wiener's random function and other Laplacian random functions. In: Proc. 2nd Berkeley Sympos. Math. Stat. Prob., University of California Press, Berkeley, CA, 1951, 171–186.Google Scholar
[44] Lévy, P., Processus Stochastiques et Mouvement Brownien. Gauthier-Villars, Paris, 1965 (1st edition, 1948).Google Scholar
[45] Magiera, R., Sequential estimation for the generalized exponential hyperbolic secant process. Statistics (2) 19 (1988), 271–281.Google Scholar
[46] Montroll, E. W., Markov chains and quantum theory. Comm. Pure and Appl. Math. 5 (1952), 415–453.Google Scholar
[47] Morris, C. N., Natural exponential families with quadratic variance functions. Ann. Statist. (1) 10 (1982), 65–80.Google Scholar
[48] Pakes, A. G., On characterizations through mixed sums. Austral. J. Statist. (2) 34 (1992), 323–339.Google Scholar
[49] Pakes, A. G., Length biasing and laws equivalent to the log-normal. J. Math. Anal. Appl. (3) 197 (1996), 825–854.Google Scholar
[50] Pakes, A. G. and Khattree, R., Length-biasing, characterizations of laws and the moment problem. Austral. J. Statist. (2) 34 (1992), 307–322.Google Scholar
[51] Pakes, A. G., Sapatinas, T. and Fosam, E. B., Characterizations, length-biasing, and infinite divisibility. Statist. Papers (1) 37 (1996), 53–69.Google Scholar
[52] Pitman, J., Cyclically stationary Brownian local time processes. Probab. Theory Related Fields 106:299–329, 1996.Google Scholar
[53] Pitman, J. and Yor, M., A decomposition of Bessel bridges. Z.Wahrsch. Verw. Gebiete 59 (1982), 425–457.Google Scholar
[54] Pitman, J. and Yor, M., Arcsine laws and interval partitions derived from a stable subordinator. Proc. LondonMath. Soc. (3) 65 (1992), 326–356.Google Scholar
[55] Pitman, J. and Yor, M., Decomposition at the maximum for excursions and bridges of one-dimensional diffusions. In: It . o's Stochastic Calculus and Probability Theory (eds. N. Ikeda, S. Watanabe, M. Fukushima and H. Kunita), Springer-Verlag, 1996, 293–310.Google Scholar
[56] Pitman, J. and Yor, M., Quelques identités en loi pour les processus de Bessel. Hommage à P. A. Meyer et J. Neveu, Astérisque 236 (1996), 249–276.Google Scholar
[57] Pitman, J. and Yor, M., The two-parameter Poisson-Dirichlet distribution derived from a stable subordinator. Ann. Probab. 25 (1997), 855–900.Google Scholar
[58] Ray, D. B., Sojourn times of a diffusion process. Illinois J. Math. 7 (1963), 615–630.Google Scholar
[59] Revuz, D. and Yor, M., Continuous martingales and Brownian motion. 3rd edition, Springer, Berlin-Heidelberg, 1999.Google Scholar
[60] Rogers, L. C. G., Williams’ characterization of the Brownian excursion law: proof and applications. In: Séminaire de Probabilités XV, Lecture Notes inMath. 850, Springer-Verlag, Berlin-New York, 1981, 227–250.Google Scholar
[61] Rogers, L. C. G. and Williams, D., Diffusions, Markov Processes and Martingales, Vol. II: It.o Calculus. Wiley, 1987.Google Scholar
[62] Sato, K., Lévy processes and infinitely divisible distributions. Cambridge University Press, Cambridge, 1999 (translated from the 1990 Japanese original, revised by the author).Google Scholar
[63] Schoutens, W., Stochastic Processes and Orthogonal Polynomials. Lecture Notes in Statistics 146, Springer, New York, 2000.Google Scholar
[64] Schoutens, W. and Teugels, J. L., Lévy processes, polynomials and martingales. Comm. Statist. Stochastic Models (1–2) 14, 335–349 (special issue in honor of Marcel F. Neuts).Google Scholar
[65] Shiga, T. and Watanabe, S., Bessel diffusions as a one-parameter family of diffusion processes. Z.Wahrsch. Verw. Gebiete 27 (1973), 37–46.Google Scholar
[66] Smith, L. and Diaconis, P., Honest Bernoulli excursions. J. Appl. Probab. 25 (1988), 464–477.Google Scholar
[67] Urbanik, K., Moments of sums of independent random variables. In: Stochastic processes. A festschrift in honour of Gopinath Kallianpur (eds. S. Cambanis, J. K. Ghosh, R. L. Karandikar and P. K. Sen), Springer, New York, 1993, 321–328.Google Scholar
[68] van Harn, K. and Steutel, F. W., Infinite divisibility and the waiting-time paradox. Comm. Statist. Stochastic Models (3) 11 (1995), 527–540.Google Scholar
[69] Vervaat, W., On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. in Appl. Probab. 11(1979), 750–783.Google Scholar
[70] Watanabe, S., Poisson point process of Brownian excursions and its applications to diffusion processes. In: Probability (Proc. Sympos. Pure Math. Vol. XXXI, University of Illinois, Urbana, Ill., 1976), Amer.Math. Soc., Providence, R.I., 1977, 153–164.Google Scholar
[71] Weil, A., Prehistory of the zeta-function. In: Number theory, trace formulas and discrete groups (Oslo, 1987), Academic Press, Boston, MA, 1989, 1–9.Google Scholar
[72] Williams, D., Decomposing the Brownian path. Bull. Amer.Math. Soc. 76 (1970), 871–873.Google Scholar
[73] Williams, D., Path decomposition and continuity of local time for one dimensional diffusions I. Proc. LondonMath. Soc. (3) 28 (1974), 738–768.Google Scholar
[74] Williams, D., Diffusions, Markov Processes and Martingales, Volume 1. Wiley, 1979.Google Scholar
[75] Williams, D., Brownian motion and the Riemann zeta-function. In: Disorder in Physical Systems (eds. G. R. Grimmett and D. J. A.Welsh), Clarendon Press, Oxford, 1990, 361–372.Google Scholar
[76] Yor, M., Some Aspects of Brownian Motion, Part II: Some Recent Martingale Problems. Lectures in Math. ETH Zürich, Birkhaüser, Basel, 1997.Google Scholar