No CrossRef data available.
Article contents
Integral Formula for Spectral Flow for 
$p$-Summable Operators
Part of:
$K$-theory and operator algebras
Infinite-dimensional manifolds
Selfadjoint operator algebras
Published online by Cambridge University Press: 07 January 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Fix a von Neumann algebra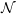 
${\mathcal{N}}$ equipped with a suitable trace 
$\unicode[STIX]{x1D70F}$. For a path of self-adjoint Breuer–Fredholm operators, the spectral flow measures the net amount of spectrum that moves from negative to non-negative. We consider specifically the case of paths of bounded perturbations of a fixed unbounded self-adjoint Breuer–Fredholm operator affiliated with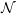 
${\mathcal{N}}$. If the unbounded operator is 
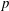$p$-summable (that is, its resolvents are contained in the ideal 
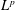$L^{p}$), then it is possible to obtain an integral formula that calculates spectral flow. This integral formula was first proved by Carey and Phillips, building on earlier approaches of Phillips. Their proof was based on first obtaining a formula for the larger class of 
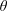$\unicode[STIX]{x1D703}$-summable operators, and then using Laplace transforms to obtain a 
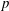$p$-summable formula. In this paper, we present a direct proof of the 
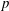$p$-summable formula that is both shorter and simpler than theirs.
MSC classification
Primary:
19K56: Index theory
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
Benameur, Moulay-Tahar, Carey, Alan L., Phillips, John, Rennie, Adam, Sukochev, Fyodor A., and Wojciechowski, Krzysztof P.,
An analytic approach to spectral flow in von Neumann algebras
. In: Analysis, geometry and topology of elliptic operators, World Sci. Publ., Hackensack, NJ, 2006.Google Scholar
Breuer, Manfred,
Fredholm theories in von Neumann algebras. I
. Math. Ann.
178(1968), 243–254. https://doi.org/10.1007/BF01350663.Google Scholar
Connes, Alain,
Compact metric spaces, Fredholm modules, and hyperfiniteness
. Ergodic Theory Dynam. Systems
9(1989), 207–220. https://doi.org/10.1017/S0143385700004934.Google Scholar
Carey, Alan and Phillips, John,
Unbounded Fredholm modules and spectral flow
. Canad. J. Math.
50(1998), 673–718. https://doi.org/10.4153/CJM-1998-038-x.Google Scholar
Carey, Alan and Phillips, John,
Spectral flow in Fredholm modules, eta invariants and the JLO cocycle
. K-Theory
31(2004), 135–194. https://doi.org/10.1023/B:KTHE.0000022922.68170.61.Google Scholar
Carey, Alan, Phillips, John, Rennie, Adam, and Sukochev, Fyodor,
The local index formula in semifinite von Neumann algebras I: spectral flow
. Adv. Math.
202(2006), 451–516. https://doi.org/10.1016/j.aim.2005.03.011.Google Scholar
Carey, Alan, Phillips, John, Rennie, Adam, and Sukochev, Fyodor,
The local index formula in semifinite von Neumann algebras II: the even case
. Adv. Math.
202(2006), 517–554. https://doi.org/10.1016/j.aim.2005.03.010.Google Scholar
Carey, Alan, Phillips, John, Rennie, Adam, and Sukochev, Fyodor,
The Chern character of semifinite spectral triples
. J. Noncommut. Geom.
2(2008), 141–193. https://doi.org/10.4171/JNCG/18.Google Scholar
Carey, Alan, Potapov, Denis, and Sukochev, Fedor,
Spectral flow is the integral of one-forms on the Banach manifold of self-adjoint Fredholm operators
. Adv. Math.
222(2009), 1809–1849. https://doi.org/10.1016/j.aim.2009.06.020.Google Scholar
Dodds, P. G., Dodds, T. K., and Sukochev, F. A.,
On p-convexity and q-concavity in non-commutative symmetric spaces
. Integral Equations Operator Theory
78(2014), 91–114. https://doi.org/10.1007/s00020-013-2082-0.Google Scholar
Dixmier, Jacques,
Applications ♮ dans les anneaux d’opérateurs
. Compositio Math.
10(1952), 1–55.Google Scholar
Dixmier, Jacques,
Remarques sur les applications ♮
. Archiv. Math.
3(1952), 290–297. https://doi.org/10.1007/BF01899229.Google Scholar
Dixmier, Jacques,
Formes linéaires sur un anneau d’opérateurs
. Bull. Soc. Math. France
81(1953), 9–39. https://doi.org/10.24033/bsmf.1436.Google Scholar
Dixmier, Jacques,
Von Neumann algebras
. North-Holland Mathematical Library, 27. North-Holland, Amsterdam, 1981.Google Scholar
Fack, Thierry and Kosaki, Hideki,
Generalized s-numbers of -measurable operators
. Pacific J. Math.
123(1986), 269–300. https://doi.org/10.2140/pjm.1986.123.269.Google Scholar
Georgescu, Magdalena C., Spectral flow in semifinite von Neumann algebras. Ph.D. thesis, University of Victoria, 2013.Google Scholar
Kalton, N. J. and Sukochev, F. A.,
Symmetric norms and spaces of operators
. J. Reine Angew. Math.
621(2008), 81–121. https://doi.org/10.1515/CRELLE.2008.059.Google Scholar
Lang, Serge,
Differential and Riemannian manifolds
. Third edition.
Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4612-4182-9.Google Scholar
Pedersen, Gert K.,
C
∗-algebras and their automorphism groups
. London Mathematical Society Monographs, 14. Academic Press, London, 1979.Google Scholar
Phillips, John,
Self-adjoint Fredholm operators and spectral flow
. Canad. Math Bull.
39(1996), 460–467. https://doi.org/10.4153/CMB-1996-054-4.Google Scholar
Phillips, John,
Spectral flow in type I and II factors—a new approach
. Fields Inst. Commun., 17. Amer. Math. Soc., Providence, RI, 1997, pp. 137–153.Google Scholar
Phillips, John and Raeburn, Iain,
An index theorem for Toeplitz operators with noncommutative symbol space
. J. Funct. Anal.
120(1994), 239–263. https://doi.org/10.1006/jfan.1994.1032.Google Scholar
Sukochev, F.,
Hölder inequality for symmetric operator spaces and trace property of K-cycles
. Bull. Lond. Math. Soc.
48(2016), 637–647. https://doi.org/10.1112/blms/bdw022.Google Scholar
You have
Access