Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T05:30:08.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Intégrales orbitales tordues sur GL(n, F) et corps locaux proches : applications

Published online by Cambridge University Press:  20 November 2018

Guy Henniart  and
Bertrand Lemaire
Guy Henniart
Affiliation:
Département de Mathématiques et UMR 8628 du CNRS, Université de Paris-Sud, bât. 425, 91405 Orsay cedex, France e-mail: Guy.Henniart@math.u-psud.fr, Bertrand.Lemaire@math.u-psud.fr
Bertrand Lemaire
Affiliation:
Département de Mathématiques et UMR 8628 du CNRS, Université de Paris-Sud, bât. 425, 91405 Orsay cedex, France e-mail: Guy.Henniart@math.u-psud.fr, Bertrand.Lemaire@math.u-psud.fr
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient 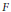$F$ un corps commutatif localement compact non archimédien, 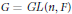$G=GL(n,F)$ pour un entier 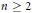$n\ge 2$, et $\kappa$ un caractère de 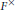${{F}^{\times }}$ trivial sur 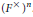${{\left( {{F}^{\times }} \right)}^{n}}$. On prouve une formule pour les $\kappa$-intégrales orbitales régulières sur 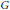$G$ permettant, si 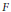$F$ est de caractéristique 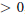$>0$, de les relever à la caractéristique nulle. On en déduit deux résultats nouveaux en caractéristique 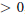$>0$ : le “lemme fondamental” pour l’induction automorphe, et une version simple de la formule des traces tordue locale d’Arthur reliant $\kappa$-intégrales orbitales elliptiques et caractères $\kappa$-tordus. Cette formule donne en particulier, pour une série $\kappa$-discrète de 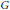$G$, les $\kappa$-intégrales orbitales elliptiques d’un pseudo-coefficient comme valeurs du caractère $\kappa$-tordu.

Keywords

22E50corps localreprésentation lisseintégrale orbitale tordueinduction automorphelemme fondamentalformule des traces localepseudo-coefficient
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 6 , 01 December 2006 , pp. 1229 - 1267
Copyright
Copyright © Canadian Mathematical Society 2006

References

Références

[A] Arthur, J., On the Fourier transforms of weighted orbital integrals. J. Reine Angew. Math. 452(1994), 163–217.Google Scholar
[BD] Bernstein, I. et Deligne, P., Le “centre” de Bernstein. Dans: Représentations des groupes réductifs sur un coprs local. Hermann, Paris, 1984, pp. 33–117.Google Scholar
[B] Bushnell, C., Representations of reductive p-adic groups: localization of Hecke algebras and applications. J. London Math. Soc. (2) 63(2001), no. 2, 364–386.Google Scholar
[BH1] Bushnell, C. et Henniart, G., The essentially tame local Langlands correspondance. I. J. Amer. Math. Soc. 18(2005), no. 3, 685–710.Google Scholar
[BH2] Bushnell, C. et Henniart, G., The essentially tame local Langlands correspondance. II. Comp. Math. 141(2005), 979–1011.Google Scholar
[BK] Bushnell, C. et Kutzko, P., The admissible dual of GL(N) via open compact subgroups. Annals of Mathematical Studies 129, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[D] Deligne, P., Les corps locaux de caractéristique p, limites de corps locaux de caractéristique 0. Dans: Représentations des groupes réductifs sur un corps local, Travaux en cours, Hermann, Paris, 1984, pp. 119–157.Google Scholar
[Ha] Hales, T., Unipotent representations and unipotent classes in SL(n). Amer. J. Math. 115(1993), no. 6, 1347–1384.Google Scholar
[Ho] Howe, R., Harish-Chandra homomorphism for p-adic groups. CBMS Regional Conference Series in Mathematics 59, American Mathematical Society, Providence, RI, 1985.Google Scholar
[HC1] Harish-Chandra, , Harmonic Analysis on Reductive p-Adic Groups. Lecture Notes in Mathematics 162, Springer-Verlag, Berlin, 1970.Google Scholar
[HC2] Harish-Chandra, , Harmonic analysis on reductive p-adic groups. Dans: Harmonic analysis on homogeneous spaces, American Mathematical Society, Providence, RI, 1972, pp. 167–192.Google Scholar
[HC3] Harish-Chandra, , A submersion principle and its applications. Dans: Geometry and Analysis, Indian Academy of Sciences, Bangalore, 1990, pp. 95–102.Google Scholar
[HH] Henniart, G. et Herb, R., Automorphic induction for GL(n)(over local non-archimedean fields) . Duke Math. J. 78(1995), no. 1, 131–192.Google Scholar
[HL1] Henniart, G. et Lemaire, B., Existence de pseudo-coefficients pour les caractères tordus des séries κ-discrètes de GL(n, F)., manuscrit.Google Scholar
[HL2] Henniart, G et Lemaire, B., Sur l’induction automorphe I: formules de caractères, en préparation.Google Scholar
[HL3] Henniart, G et Lemaire, B., Le lemme fondamental pour l’induction automorphe en caractéristique nulle, en préparation.Google Scholar
[L1] Lemaire, B., Intégrales orbitales su. GL(n) et corps locaux proches. Ann. Institut Fourier 46(1996), no. 4, 1027–1056.Google Scholar
[L2] Lemaire, B., Intégrales orbitales sur GL(n, F) où F est un corps local non archimédien. Mém. Soc. Math. France 70, 1997.Google Scholar
[L3] Lemaire, B., Représentations génériques d. GL n et corps locaux proches. J. Algebra 236(2001), no. 2, 549–574.Google Scholar
[L4] Lemaire, B., Intégrabilité locale des caractères de SL n (D), to appear in Pacific J. Math.Google Scholar
[S] Serre, J.-P., Corps locaux. (Troisième édition, corrigée), Hermann, Paris, 1968.Google Scholar
[W] Waldspurger, J.-L., Sur les intégrales orbitales tordues pour les groupes linéaires: un lemme fondamental. J. Canad. Math. 43(1991), no. 4, 852–896.Google Scholar