Article contents
Interpolation between noncommutative martingale Hardy and BMO spaces: the case 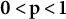 $\textbf {0<p<1}$
$\textbf {0<p<1}$
Published online by Cambridge University Press: 25 August 2021
Abstract
Let
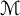 $\mathcal {M}$
be a semifinite von Nemann algebra equipped with an increasing filtration
$\mathcal {M}$
be a semifinite von Nemann algebra equipped with an increasing filtration
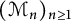 $(\mathcal {M}_n)_{n\geq 1}$
of (semifinite) von Neumann subalgebras of
$(\mathcal {M}_n)_{n\geq 1}$
of (semifinite) von Neumann subalgebras of
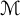 $\mathcal {M}$
. For
$\mathcal {M}$
. For
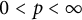 $0<p <\infty $
, let
$0<p <\infty $
, let
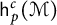 $\mathsf {h}_p^c(\mathcal {M})$
denote the noncommutative column conditioned martingale Hardy space and
$\mathsf {h}_p^c(\mathcal {M})$
denote the noncommutative column conditioned martingale Hardy space and
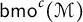 $\mathsf {bmo}^c(\mathcal {M})$
denote the column “little” martingale BMO space associated with the filtration
$\mathsf {bmo}^c(\mathcal {M})$
denote the column “little” martingale BMO space associated with the filtration
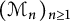 $(\mathcal {M}_n)_{n\geq 1}$
.
$(\mathcal {M}_n)_{n\geq 1}$
.
We prove the following real interpolation identity: if
 $0<p <\infty $
and
$0<p <\infty $
and
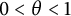 $0<\theta <1$
, then for
$0<\theta <1$
, then for
 $1/r=(1-\theta )/p$
,
$1/r=(1-\theta )/p$
,
 $$ \begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*} $$
$$ \begin{align*} \big(\mathsf{h}_p^c(\mathcal{M}), \mathsf{bmo}^c(\mathcal{M})\big)_{\theta, r}=\mathsf{h}_{r}^c(\mathcal{M}), \end{align*} $$
For the case of complex interpolation, we obtain that if
 $0<p<q<\infty $
and
$0<p<q<\infty $
and
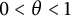 $0<\theta <1$
, then for
$0<\theta <1$
, then for
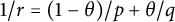 $1/r =(1-\theta )/p +\theta /q$
,
$1/r =(1-\theta )/p +\theta /q$
,
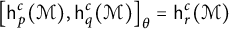 $$ \begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*} $$
$$ \begin{align*} \big[\mathsf{h}_p^c(\mathcal{M}), \mathsf{h}_q^c(\mathcal{M})\big]_{\theta}=\mathsf{h}_{r}^c(\mathcal{M}) \end{align*} $$
These extend previously known results from
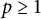 $p\geq 1$
to the full range
$p\geq 1$
to the full range
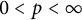 $0<p<\infty $
. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned
$0<p<\infty $
. Other related spaces such as spaces of adapted sequences and Junge’s noncommutative conditioned
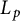 $L_p$
-spaces are also shown to form interpolation scale for the full range
$L_p$
-spaces are also shown to form interpolation scale for the full range
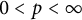 $0<p<\infty $
when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned
$0<p<\infty $
when either the real method or the complex method is used. Our method of proof is based on a new algebraic atomic decomposition for Orlicz space version of Junge’s noncommutative conditioned
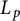 $L_p$
-spaces.
$L_p$
-spaces.
We apply these results to derive various inequalities for martingales in noncommutative symmetric quasi-Banach spaces.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
References
- 7
- Cited by



