Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T06:13:17.052Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant Einstein Metrics on Some Homogeneous Spaces of Classical Lie Groups

Published online by Cambridge University Press:  20 November 2018

Andreas Arvanitoyeorgos ,
V. V. Dzhepko  and
Yu. G. Nikonorov
Andreas Arvanitoyeorgos
Affiliation:
University of Patras, Department of Mathematics, GR-26500 Rion, Greece email: arvanito@math.upatras.gr
V. V. Dzhepko
Affiliation:
Rubtsovsk Industrial Institute, ul. Traktornaya, 2/6, Rubtsovsk, 658207, Russia email: J Valera V@mail.runik@inst.rubtsovsk.ru
Yu. G. Nikonorov
Affiliation:
Rubtsovsk Industrial Institute, ul. Traktornaya, 2/6, Rubtsovsk, 658207, Russia email: J Valera V@mail.runik@inst.rubtsovsk.ru
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

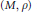A Riemannian manifold $\left( M,\,\rho \right)$ is called Einstein if the metric $\rho $ satisfies the condition 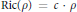$\text{Ric}\left( \rho \right)\,=\,c\,\cdot \,\rho $ for some constant $c$. This paper is devoted to the investigation of $G$-invariant Einstein metrics, with additional symmetries, on some homogeneous spaces 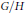$G/H$ of classical groups. As a consequence, we obtain new invariant Einstein metrics on some Stiefel manifolds 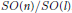$SO\left( n \right)/SO\left( l \right)$. Furthermore, we show that for any positive integer 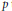$p$ there exists a Stiefel manifold 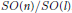$SO\left( n \right)/SO\left( l \right)$ that admits at least 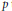$p$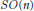$SO\left( n \right)$-invariant Einstein metrics.

Keywords

53C2553C30Riemannian manifoldshomogeneous spacesEinstein metricsStiefel manifolds
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1201 - 1213
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Alekseevsky, D. V., Dotti, I., and Ferraris, C., Homogeneous Ricci positive 5-manifolds, Pacific J. Math. 175(1996), no. 1, 1–12.Google Scholar
[2] Arvanitoyeorgos, A., New invariant Einstein metrics on generalized flag manifolds. Trans. Amer. Math. Soc. 337(1993), no. 2, 981–995.Google Scholar
[3] Back, A. and Hsiang, W. Y., Equivariant geometry and Kervaire spheres. Trans. Amer. Math. Soc. 304(1987) no. 1, 207–227.Google Scholar
[4] Besse, A., Einstein Manifolds. Ergebnisse der mathematik und ihrer Grenzgebiete 10, Springer-Verlag, Berlin, 1987.Google Scholar
[5] Böhm, C., Homogeneous Einstein metrics and simplicial complexes. J. Differential Geom. 67(2004), no. 1, 79–165.Google Scholar
[6] Böhm, C. and Kerr, M., Low-dimensional homogenous Einstein manifolds. Trans. Amer. Math. Soc. 358(2006), no. 4, 1455–1468.Google Scholar
[7] Böhm, C., Wang, M., and Ziller, W., A variational approach for compact homogeneous Einstein manifolds. Geom. Func. Anal. 14(2004), no. 4, 681–733.Google Scholar
[8] D’Atri, J. E. and Nickerson, N., Geodesic symmetries in space with special curvature tensors, J. Diff. Geom. 9 (1974) 251–262.Google Scholar
[9] D’Atri, J. E. and Ziller, W., Naturally reductive metrics and Einstein metrics on compact Lie groups. Memoirs Amer. Math. Soc. 18(1979) no. 215.Google Scholar
[10] Jensen, G., The scalar curvature of left-invariant Riemannian metrics. Indiana J. Math. 20(1971) 1125–1144.Google Scholar
[11] Jensen, G., Einstein metrics on principal fiber bundles J. Differential Geom. 8(1973), 599–614.Google Scholar
[12] Kerr, M., New examples of homogeneous Einstein metrics. Michigan J. Math. 45(1998)no. 1, 115–134.Google Scholar
[13] Kobayashi, S., Topology of positive pinched Kähler manifolds. Tôhoku Math. J. 15(1963), 121–139.Google Scholar
[14] Kimura, M., Homogeneous Einstein metrics on certain Kähler C-spaces. In: Recent Topics in Differential and Analytic Geometry. Adv. Stud. Pure Math. 18-I. Academic Press, Boston, MA, 1990, pp. 303–320.Google Scholar
[15] Lomshakov, A. V., Nikonorov, Yu. G., and Firsov, E. V., Invariant Einstein metrics on three-locally-symmetric spaces. (Russian) Mat. Tr. 6(2003), no. 2, 80–101; Engl. transl. in Siberian Adv. Math. 14(2004), no. 3, 43–62.Google Scholar
[16] Sagle, A., Some homogeneous Einstein manifolds. Nagoya Math. J. 39(1970), 81–106.Google Scholar
[17] Nikonorov, Yu. G., On a class of homogeneous compact Einstein manifolds. (Russian) Sibirsk. Mat. Zh. 41(2000), no. 1, 200–205; Engl. transl. in Siberian Math. J. 41(2000), no. 1, 168–172.Google Scholar
[18] Sakane, Y., Homogeneous Einstein metrics on flag manifolds. Lobachevskii J. Math. 4(1999), 71–87.Google Scholar
[19] N., Wallach: Compact homogeneous riemannian manifolds with strictly positive curvature, Ann. math. 96 (1972) 277–295.Google Scholar
[20] Wang, M., Einstein metrics from symmetry and Bundle constructions. In: Surveys in Differential Geometry: Essays on Einstein Manifolds. Surv. Differ. Geom. VI, Int. Press, Boston, MA, 1999, pp. 287–325.Google Scholar
[21] Wang, M.and Ziller, W., Existence and non-existence of homogeneous Einstein metrics. Invent. Math. 84(1986), no. 1, 177–194.Google Scholar
[22] Wang, M., Einstein metrics with positive scalar curvature. In: Curvature and Topology of Riemannian Manifolds, Springer Lecture Notes in Mathematics 1201, Springer, Berlin, 1986, pp. 319–336.Google Scholar