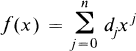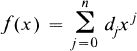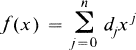Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Murty, M. Ram
2002.
Prime Numbers and Irreducible Polynomials.
The American Mathematical Monthly,
Vol. 109,
Issue. 5,
p.
452.
Bonciocat, Nicolae Ciprian
and
Zaharescu, Alexandru
2008.
Irreducible multivariate polynomials obtained from polynomials in fewer variables.
Journal of Pure and Applied Algebra,
Vol. 212,
Issue. 10,
p.
2338.
Bonciocat, Anca Iuliana
and
Bonciocat, Nicolae Ciprian
2009.
The Irreducibility of Polynomials That Have One Large Coefficient and Take a Prime Value.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 4,
p.
511.
Filaseta, Michael
and
Gross, Samuel
2014.
49598666989151226098104244512918.
Journal of Number Theory,
Vol. 137,
Issue. ,
p.
16.
Phetnun, Phitthayathon
Kanasri, Narakorn Rompurk
Singthongla, Patiwat
and
Solovjovs, Sergejs
2021.
On the Irreducibility of Polynomials Associated with the Complete Residue Systems in any Imaginary Quadratic Fields.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2021,
Issue. ,
p.
1.
Bonciocat, Anca Iuliana
Bonciocat, Nicolae Ciprian
Bugeaud, Yann
and
Cipu, Mihai
2022.
Apollonius circles and irreducibility criteria for polynomials.
Indagationes Mathematicae,
Vol. 33,
Issue. 2,
p.
421.
Bonciocat, Ciprian Mircea
and
Bonciocat, Nicolae Ciprian
2022.
Zero-free angular sectors and lens-shaped regions for polynomials, with applications to irreducibility.
Communications in Algebra,
Vol. 50,
Issue. 6,
p.
2604.
Bonciocat, Nicolae Ciprian
Garg, Rishu
and
Singh, Jitender
2024.
Some factorization results for bivariate polynomials.
Communications in Algebra,
p.
1.
Mináč, Ján
Nguyen, Tung T.
and
Tân, Nguyễn Duy
2024.
On the Arithmetic of Generalized Fekete Polynomials.
Experimental Mathematics,
Vol. 33,
Issue. 4,
p.
723.