Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goodaire, E. G.
1974.
Weighted representations of a primitive algebra.
Proceedings of the American Mathematical Society,
Vol. 42,
Issue. 1,
p.
61.
Goodaire, Edgar G.
1978.
A classification of jordan bimodules by weights.
Communications in Algebra,
Vol. 6,
Issue. 9,
p.
887.

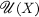 of a (not necessarily associative) algebra
of a (not necessarily associative) algebra 