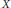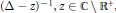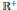Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, Hart F.
and
Zworski, Maciej
2016.
Heat traces and existence of scattering resonances for bounded potentials.
Annales de l'Institut Fourier,
Vol. 66,
Issue. 2,
p.
455.
Christiansen, T. J.
2019.
Resonant Rigidity for Schrödinger Operators in Even Dimensions.
Annales Henri Poincaré,
Vol. 20,
Issue. 5,
p.
1543.
Christiansen, T. J.
2023.
Resonances for Schrödinger operators on
infinite cylinders and other products.
Analysis & PDE,
Vol. 16,
Issue. 7,
p.
1497.