Karamata Renewed and Local Limit Results

Abstract

Connections between behaviour of real analytic functions (with no negative Maclaurin series coefficients and radius of convergence one) on the open unit interval, and to a lesser extent on arcs of the unit circle, are explored, beginning with Karamata's approach. We develop conditions under which the asymptotics of the coefficients are related to the values of the function near 1; specifically, 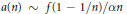$a(n)\sim f(1-1/n)/\alpha n$ (for some positive constant 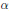$\alpha $), where 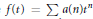$f\left( t \right)=\sum{a}\left( n \right){{t}^{n}}$. In particular, if 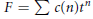$F=\sum{c\left( n \right){{t}^{n}}}$ where 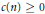$c(n)\ge 0$ and 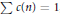$\Sigma c(n)=1$, then 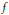$f$ defined as 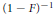${{\left( 1-F \right)}^{-1}}$ (the renewal or Green's function for 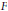$F$) satisfies this condition if 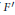${F}'$ does (and a minor additional condition is satisfied). In come cases, we can show that the absolute sum of the differences of consecutive Maclaurin coefficients converges. We also investigate situations in which less precise asymptotics are available.