No CrossRef data available.
Article contents
k-Discreteness and k-Analytic Sets
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
All spaces considered here are metrizable. k will always denote an infinite cardinal. The successor of k will be denoted by k+.
Of particular interest will be the Baire spaces 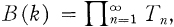 where each Tn is a discrete space of cardinal k. The product topology on B(k) is the same as the topology given by the (complete) “first-difference” metric, p : p(s, t) = 1/n if Si = ti for 1 ≦ i ≦ n —1 and sn = tn. A great deal of information about these spaces can be found in [4].
where each Tn is a discrete space of cardinal k. The product topology on B(k) is the same as the topology given by the (complete) “first-difference” metric, p : p(s, t) = 1/n if Si = ti for 1 ≦ i ≦ n —1 and sn = tn. A great deal of information about these spaces can be found in [4].
A subset A of X is called k-analytic (in X) if there exist, for each t ∈ B(k), closed subsets F(t1), …, F(t 1, …, tn), … of X such that
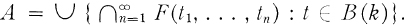
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1980
References
1.
El'kin, A., A-sets in complete metric spaces, Soviet Math. Dokl. 8 (1967), 874–877.Google Scholar
2.
Hansell, R., Borel measurable mappings for nonseparable metric spaces, Trans. Amer. Math. Soc. 161 (1971), 145–169.Google Scholar
3.
Lasnev, N., Continuous decompositions of collectively normal spaces, Soviet Math. Dokl. 188 (1967), 1069–70.Google Scholar
6.
Stone, A. H., On a-discreteness and Borel isomorphism, Amer. J. Math. 85 (1963), 655–666.Google Scholar
7.
Stone, A. H., Kernel constructions and Borel sets, Trans. Amer. Math. Soc. 107 (1963), 58–70.Google Scholar
9.
Pol, R., Note on decompositions of metrizable spaces, I, Fund. Math. 95 (1977), 95–103.Google Scholar
10.
Pol, R., Note on decompositions of metrizable spaces, II, Fund. Math.
100 (2) (1978), 129–143.Google Scholar
11.
Preiss, D., Completely additive disjoint system of Baire sets is of bounded class, Comm. Math. Univ. Carolina. 15 (1975), 341–344.Google Scholar

