Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:29:39.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Korovkin Theorems for Integral Operators with Kernels of Finite Oscillation

Published online by Cambridge University Press:  20 November 2018

M. J. Marsden  and
S. D. Riemenschneider
M. J. Marsden
Affiliation:
University of Alberta, Edmonton, Alberta
S. D. Riemenschneider
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There has been considerable interest recently in the investigation of "Korovkin sets". Briefly, for X a Banach space and 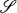a family of linear operators on X, a subset K ⊂ X is a Korovkin set relative to 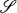if for any bounded sequence {Tn} ⊂ 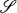, Tnk → k in X for each k ∊ K implies Tnx → x for each x ∊ X. A large portion of these investigations have been carried out for X being one of the spaces C(S), S compact Hausdorff, the usual Lp spaces of functions on some finite measure space, or some Banach lattice; while 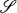is one of the classes 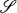+-positive operators, 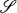1-contractions (i.e., ||T|| 1), or 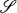+ ⋂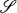1

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1390 - 1404
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Achieser, N. I., Vorlesungen über Approximationstheorie (Akademie-Verlag, Berlin, 1967).Google Scholar
2. Butzer, P. L., A survey of work on approximation at Aachen, 1968-1972. In “Approximation Theory, pp. 31-100, Proc. 1973 Austin Conf. G. G. Lorentz ed. (Academic Press, New York, 1973).Google Scholar
3. Butzer, P. L., Nessel, R. J., and K. Scherer, Trigonometric convolution operators with kernels having alternating signs and their degree of convergence, Jber. Deutsch. Math.-Verein 70 (1967), 86–99.Google Scholar
4. DeVore, R. and Richards, F., The degree of approximation by Chebyshevian Splines, Trans. Amer. Math. Soc. 181 (1973), 401–418.Google Scholar
5. Ditzian, Zeev and Freud, Geza, Linear approximating processes with limited oscillation (to appear in J. Approximation Theory).Google Scholar
6. Dzjadyk, V. K., Approximation of functions by positive linear operators and singular integrals (Russian), Mat. Sb. 70 (1966), 508–517.Google Scholar
7. Karlin, S. and Studden, W. J., Tchebycheff systems: with applications in analysis and statistics (Interscience Publishers, New York, 1966).Google Scholar
8. Korovkin, P. P., Convergent sequences of linear operators (Russian), Uspehi Mat. Nauk 17 (1962), 147–152.Google Scholar
9. Korovkin, P. P., On the order of approximation of functions by linear polynomial operators of the class , In “Studies of Contemporary Problems in the Constructive Theory of Functions“ (Proc. Second All-Union Conf. on the Constructive theory of Functions, Baku 1962), I. I. Ibragimov Editor, Acad. Sci. Azerbaijani SSR Inst. Math. Mech., Izad. Akad. Nauk Azerbaidžan SSR, Baku, 1965, 163-166.Google Scholar
10. Shapiro, H. S., Topics in approximation theory (Springer-Verlag, Berlin, 1971).Google Scholar
11. Willett, D., Disconjugacy tests for singular linear differential equations, SIAM J. Math. Anal. 2 (1971), 536–545.Google Scholar