Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T05:47:23.027Z Has data issue: false hasContentIssue false
  • English
  • Français

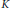$K$-theory of Furstenberg Transformation Group 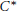${{\text{C}}^{\text{*}}}$-algebras

Published online by Cambridge University Press:  20 November 2018

Kamran Reihani
Kamran Reihani*
Affiliation:
Department of Mathematics and Statistics, Northern Arizona University, Flagstaff, AZ 86011, USA, e-mail: kamran.reihani@nau.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper studies the 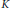$K$-theoretic invariants of the crossed product 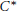${{C}^{*}}$-algebras associated with an important family of homeomorphisms of the tori 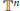${{\mathbb{T}}^{n}}$ called Furstenberg transformations. Using the Pimsner–Voiculescu theorem, we prove that given $n$, the 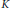$K$-groups of those crossed products whose corresponding 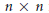$n\,\times \,n$ integer matrices are unipotent of maximal degree always have the same rank 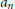${{a}_{n}}$. We show using the theory developed here that a claim made in the literature about the torsion subgroups of these 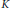$K$-groups is false. Using the representation theory of the simple Lie algebra 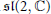$\mathfrak{s}\mathfrak{l}\left( 2,\,\mathbb{C} \right)$, we show that, remarkably, 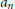${{a}_{n}}$ has a combinatorial significance. For example, every 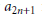${{a}_{2n+1}}$ is just the number of ways that 0 can be represented as a sum of integers between –$n$ and $n$ (with no repetitions). By adapting an argument of van Lint (in which he answered a question of Erdős), a simple explicit formula for the asymptotic behavior of the sequence 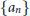$\{{{a}_{n}}\}$ is given. Finally, we describe the order structure of the 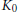${{K}_{0}}$-groups of an important class of Furstenberg crossed products, obtaining their complete Elliott invariant using classification results of H. Lin and N. C. Phillips.

Keywords

19K1419K9946L3546L8005A1505A1605A1715A3617B1017B2037B0554H20K-theorytransformation group C*-algebraFurstenberg transformationAnzai transformationminimal homeomorphismpositive coneminimal homeomorphism
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 6 , 01 December 2013 , pp. 1287 - 1319
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Anderson, J. and Paschke, W., The rotation algebra. Houston J. Math. 15(1989), no. 1, 1–26.Google Scholar
[2] Atiyah, M., K-theory. Lecture notes by D. W. Anderson. W. A. Benjamin, New York-Amsterdam, 1967.Google Scholar
[3] Blackadar, B., K-theory for operator algebras. Second ed., Mathematical Sciences Research Institute Publications, 5, Cambridge University Press, Cambridge, 1998.Google Scholar
[4] Effros, E. G. and Hahn, F., Locally compact transformation groups and C*-algebras. Mem. Amer. Math. Soc., 75, American Mathematical Society, Providence, RI, 1967.Google Scholar
[5] Entringer, R. C., Representation of m as Σn k =−n ∊kk. Canad. Math. Bull. 11(1968), 289–293. http://dx.doi.org/10.4153/CMB-1968-036-3 Google Scholar
[6] Erdős, P., Extremal problems in number theory. 1965 Proc. Sympos. Pure Math., 8, American Mathematical Society, Providence, RI, 1965, pp. 181–189.Google Scholar
[7] Exel, R., Rotation numbers for automorphisms of C*-algebras. Pacific J. Math. 127(1987), no. 1, 31–89. http://dx.doi.org/10.2140/pjm.1987.127.31 Google Scholar
[8] Furstenberg, H., Recurrence in ergodic theory and combinatorial number theory. M. B. Porter Lectures, Princeton University Press, Princeton, NJ, 1981.Google Scholar
[9] Furstenberg, H., Strict ergodicity and transformation of the torus. Amer. J. Math. 83(1961), 573–601. http://dx.doi.org/10.2307/2372899 Google Scholar
[10] Gorbatsevich, V. V., Onishchik, A. L., and Vinberg, E. B., Foundations of Lie theory and Lie transformation groups. Encyclopaedia of Mathematical Sciences, 20, Springer-Verlag, Berlin, 1997.Google Scholar
[11] Greub, W., Multilinear algebra. Second ed., Universitext, Springer-Verlag, New York-Heidelberg, 1978.Google Scholar
[12] Hahn, F. J., On affine transformations of compact abelian groups. Amer. J. Math. 85(1963), 428–446. http://dx.doi.org/10.2307/2373133 Google Scholar
[13] Hahn, F. J. and Parry, W., Minimal dynamical systems with quasi-discrete spectrum. J. London Math. Soc. 40(1965), 309–323. http://dx.doi.org/10.1112/jlms/s1-40.1.309 Google Scholar
[14] Hodgkin, L., On the K-theory of Lie groups. Topology, 6(1967), 1–36. http://dx.doi.org/10.1016/0040-9383(67)90010-9 Google Scholar
[15] Humphreys, J. E., Introduction to Lie algebras and representation theory. Second printing, revised, Graduate Texts in Mathematics, 9, Springer-Verlag, New York-Berlin, 1978.Google Scholar
[16] Ji, R., On the crossed product C*-algebras associated with Furstenberg transformations on tori. Thesis (Ph.D.), State University of New York at Stony Brook, ProQuest LLC, Ann Arbor, MI, 1986.Google Scholar
[17] Karoubi, M., K-theory. An introduction. Grundlehren der Mathematischen Wissenschaften, 226, Springer-Verlag, Berlin-New York, 1978.Google Scholar
[18] Kodaka, K., The positive cones of K0-groups of crossed products associated with Furstenberg transformations on the 2-torus. Proc. Edinburgh Math. Soc. (2) 43(2000), no. 1, 167–175. http://dx.doi.org/10.1017/S0013091500020782 Google Scholar
[19] Lin, H., Classification of simple C*-algebras of tracial topological rank zero. Duke Math. J. 125(2004), no. 1, 91–119. http://dx.doi.org/10.1215/S0012-7094-04-12514-X Google Scholar
[20] Lin, Q. and Phillips, N. C., Direct limit decomposition for C*-lgebras of minimal diffeomorphisms. In: Operator algebras and applications, Adv. Stud. Pure Math., 38, Math. Soc. Japan, Tokyo, 2004, pp. 107–133.Google Scholar
[21] Lin, Q., Crossed products by minimal homeomorphisms. J. Reine Angew. Math. 641(2010), 95–122.Google Scholar
[22] Lin, Q., Ordered K-theory for C*-algebras of minimal homeomorphisms. In: Operator algebras and operator theory (Shanghai, 1997), Contemp. Math., 228, American Mathematical Society, Providence, RI, 1998, pp. 298–314.Google Scholar
[23] van Lint, J. H., Representations of 0 as Σn k =−n ∊kk. Proc. Amer. Math. Soc. 18(1967), 182–184. http://dx.doi.org/10.1090/S0002-9939-1967-0205964-8 Google Scholar
[24] Milnes, P., Groups and C*-algebras from a 4-dimensional Anzai flow. Math. Nachr. 235(2002), 129–141. http://dx.doi.org/10.1002/1522-2616(200202)235:1h129::AID-MANA129i3.0.CO;2-S Google Scholar
[25] Milnes, P. and Walters, S., Simple quotients of the group C*-algebra of a discrete 4-dimensional nilpotent group. Houston J. Math. 19(1993), no. 4, 615–636.Google Scholar
[26] Milnes, P., Simple infinite dimensional quotients of C*(G) for discrete 5-dimensional nilpotent groups G. Illinois J. Math. 41(1997), no. 2, 315–340.Google Scholar
[27] Newman, M., Integral matrices. Pure and Applied Mathematics, 45, Academic Press, New York-London, 1972.Google Scholar
[28] Packer, J. A., K-theoretic invariants for C*-algebras associated to transformations and induced flows. J. Funct. Anal. 67(1986), no. 1, 25–59. http://dx.doi.org/10.1016/0022-1236(86)90042-X Google Scholar
[29] Phillips, N. C., Cancellation and stable rank for direct limits of recursive subhomogeneous algebras. Trans. Amer. Math. Soc. 359(2007), no. 10, 4625–4652. http://dx.doi.org/10.1090/S0002-9947-07-03849-4 Google Scholar
[30] Phillips, N. C., Examples of different minimal diffeomorphisms giving the same C*-algebras. Israel J. Math. 160(2007), 189–217. http://dx.doi.org/10.1007/s11856-007-0061-3 Google Scholar
[31] Pimsner, M. and Voiculescu, D., Exact sequences for K-groups and Ext-groups of certain crossed product C*-algebras. J. Operator Theory 4(1980), no. 1, 93–118.Google Scholar
[32] Power, S. C., Simplicity of C*-algebras of minimal dynamical systems. J. London Math. Soc. 18(1978), no. 3, 534–538. http://dx.doi.org/10.1112/jlms/s2-18.3.534 Google Scholar
[33] Reihani, K. and Milnes, P., Analysis on discrete cocompact subgroups of the generic filiform Lie groups. Acta. Math. Hungar. 112(2006), no. 1–2, 157–179. http://dx.doi.org/10.1007/s10474-006-0059-z Google Scholar
[34] Rieffel, M. A., C*-algebras associated with irrational rotations. Pacific J. Math. 93(1981), no. 2, 415–429. http://dx.doi.org/10.2140/pjm.1981.93.415 Google Scholar
[35] Rosenberg, J., Group C*-algebras and topological invariants. In: Operator algebras and group representations, Monogr. Stud. Math., 18, Pitman, Boston, 1984, pp. 95–115.Google Scholar
[36] Schochet, C., Topological methods for C*-algebras II: Geometric resolutions and the Künneth formula. Pacific J. Math. 98(1982), no. 2, 443–458. http://dx.doi.org/10.2140/pjm.1982.98.443 Google Scholar
[37] Taylor, J. L., Banach algebras and topology. In: Algebras in analysis (Proc. Instructional Conf. and NATO Advanced Study Inst., Birmingham, 1973), Academic Press, London, 1975, pp. 118–186.Google Scholar
[38] Tomiyama, J., Invitation to C*-algebras and topological dynamics. World Scientific Advanced Series in Dynamical Systems, 3,World Scientific, Singapore, 1987.Google Scholar
[39] Walters, S., K-groups and classification of simple quotients of group C*-algebras of certain discrete 5-dimensional nilpotent groups. Pacific J. Math. 202(2002), no. 2, 491–509. http://dx.doi.org/10.2140/pjm.2002.202.491 Google Scholar