Article contents
Lambert series of logarithm, the derivative of Deninger’s function 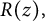 $R(z),$ and a mean value theorem for
$R(z),$ and a mean value theorem for 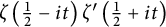 $\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
$\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )$
Published online by Cambridge University Press: 11 October 2023
Abstract
An explicit transformation for the series 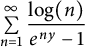 $\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$, or equivalently,
$\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$, or equivalently, 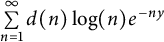 $\sum \limits _{n=1}^{\infty }d(n)\log (n)e^{-ny}$ for Re
$\sum \limits _{n=1}^{\infty }d(n)\log (n)e^{-ny}$ for Re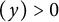 $(y)>0$, which takes y to
$(y)>0$, which takes y to 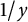 $1/y$, is obtained for the first time. This series transforms into a series containing the derivative of
$1/y$, is obtained for the first time. This series transforms into a series containing the derivative of 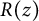 $R(z)$, a function studied by Christopher Deninger while obtaining an analog of the famous Chowla–Selberg formula for real quadratic fields. In the course of obtaining the transformation, new important properties of
$R(z)$, a function studied by Christopher Deninger while obtaining an analog of the famous Chowla–Selberg formula for real quadratic fields. In the course of obtaining the transformation, new important properties of 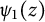 $\psi _1(z)$ (the derivative of
$\psi _1(z)$ (the derivative of 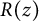 $R(z)$) are needed as is a new representation for the second derivative of the two-variable Mittag-Leffler function
$R(z)$) are needed as is a new representation for the second derivative of the two-variable Mittag-Leffler function 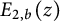 $E_{2, b}(z)$ evaluated at
$E_{2, b}(z)$ evaluated at 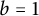 $b=1$, all of which may seem quite unexpected at first glance. Our transformation readily gives the complete asymptotic expansion of
$b=1$, all of which may seem quite unexpected at first glance. Our transformation readily gives the complete asymptotic expansion of 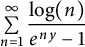 $\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$ as
$\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$ as 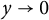 $y\to 0$ which was also not known before. An application of the latter is that it gives the asymptotic expansion of
$y\to 0$ which was also not known before. An application of the latter is that it gives the asymptotic expansion of 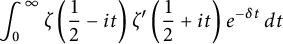 $ \displaystyle \int _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$ as
$ \displaystyle \int _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$ as 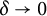 $\delta \to 0$.
$\delta \to 0$.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
Dedicated to Christopher Deninger on account of his 65th birthday
Part of this work was done when the first author was a National Postdoctoral Fellow (NPDF) at IIT Gandhinagar funded by the grant PDF/2021/001224, and later, when he was an INSPIRE faculty at IISER Kolkata supported by the DST grant DST/INSPIRE/04/2021/002753. The second author’s research is funded by the Swarnajayanti Fellowship grant SB/SJF/2021-22/08. The third author is supported by CSIR SPM Fellowship under the grant number SPM-06/1031(0281)/2018-EMR-I. All of the authors sincerely thank the respective funding agencies for their support.
References
- 1
- Cited by


