Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T14:11:10.813Z Has data issue: false hasContentIssue false
  • English
  • Français

L-Functoriality for Local Theta Correspondence of Supercuspidal Representations with Unipotent Reduction

Published online by Cambridge University Press:  20 November 2018

Shu-Yen Pan
Shu-Yen Pan*
Affiliation:
Department of Mathematics, National Tsing Hua University and National Center of Theoretical Sciences, Hsinchu 300, Taiwan e-mail: sypan@math.nthu.edu.tw
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The preservation principle of local theta correspondences of reductive dual pairs over a 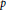$p$-adic field predicts the existence of a sequence of irreducible supercuspidal representations of classical groups. Adams and Harris-Kudla-Sweet have a conjecture about the Langlands parameters for the sequence of supercuspidal representations. In this paper we prove modified versions of their conjectures for the case of supercuspidal representations with unipotent reduction.

Keywords

22E5011F2720C33local theta correspondencesupercuspidal representationpreservation principleLanglands functoriality
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 1 , 01 February 2017 , pp. 186 - 219
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Ada89] Adams, J., L-functoriality for dual pairs. Orbites unipotentes et représentations II Astérisque 171–172(1989), 85-129.Google Scholar
[AM93] Adams, J. and Moy, A., Unipotent representations and reductive dual pairs over finite fields. Trans. Amer. Math. Soc. 340(1993), 309–321. http://dx.doi.org/10.1090/S0002-9947-1993-1173855-4 Google Scholar
[Aub91] Aubert, A.M., Description de la correspondance de Howe en termes de classification de Kazhdan-Lusztig. Invent. Math. 103(1991), 379–415. http://dx.doi.Org/10.1007/BF01239519 Google Scholar
[AMR96] Aubert, A.-M., Michel, J., and Rouquier, R., Correspondance de Howe pour les groupes réductifs sur les corps finis. Duke Math. J. 83(1996), 353–397. http://dx.doi.org/10.1215/S0012-7094-96-08312-X Google Scholar
[Bor79] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L-functions II, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence,RI, 1979, pp. 27–61.Google Scholar
[DL76] Deligne, P. and Lusztig, G., Representations of reductive groups over finite fields. Ann. of Math. (2) 103(1976), 103–161. http://dx.doi.org/10.2307/1971021 Google Scholar
[Gér77] Gérardin, P., Weil representations associated to finite fields, J. Algebra 46 (1977), 54–101. http://dx.doi.Org/10.1016/0021-8693(77)90394-5 Google Scholar
[HKS96] Harris, M., Kudla, S., and Sweet, W., Theta dichotomy for unitary groups. J. Amer. Math. Soc. 9(1996), 941–1004. http://dx.doi.org/10.1090/S0894-0347-96-00198-1 Google Scholar
[Kud86] Kudla, S., On the local theta correspondence. Invent. Math. 83(1986), 229–255. http://dx.doi.org/10.1007/BF01388961 Google Scholar
[KR94] Kudla, S. and Rallis, S., A regularized Siegel-Weil formula: the first term identity. Ann. of Math. (2) 140(1994), 1–80. http://dx.doi.org/10.2307/2118540 Google Scholar
[KR05] Kudla, S., On first occurrence in the local theta correspondence. In: Automorphic representations, L-functions and applications: progress and prospects, Ohio State Univ. Math. Res. Inst. Publ., 11, de Gruyter, Berlin, 2005, pp. 273–308. http://dx.doi.Org/10.1515/9783110892703.273 Google Scholar
[Lus77] Lusztig, G., Irreducible representations of finite classical groups. Invent. Math. 43(1977), 125–175. http://dx.doi.Org/10.1007/BF01390002 Google Scholar
[Lus83] Lusztig, G., Some examples of square integrable representations of semisimple p-adic groups. Trans. Amer. Math. Soc. 277(1983), 623–653. http://dx.doi.Org/10.2307/1999228 Google Scholar
[Lus95] Lusztig, G., Classification of unipotent representations of simple p-adic groups. Internat. Math. Res. Notices 11(1995), 517–589. http://dx.doi.Org/10.1155/S1073792895000353 Google Scholar
[LusO2] Lusztig, G. ,Classification of unipotent representations of simple p-adic groups. II.Represent.Theory 6(2002), 243–289. http://dx.doi.Org/10.1090/S1088-4165-02-00173-5 Google Scholar
[Moeg05] Moeglin, C., Stabilité pour les représentations elliptiques de réduction unipotente: le cas des groupes unitaires. In: Automorphic representations, L-functions and applications: progress and prospects, Ohio State Univ. Math. Res. Inst. Publ., 11, de Gruyter, Berlin, 2005, pp. 361–402. http://dx.doi.Org/10.1515/9783110892703.361 Google Scholar
[Mor96] Morris, L., Tamely ramified supercuspidal representations. Ann. Sci. École Norm. Sup. (4) 29(1996), 639–667.Google Scholar
[Mor99] Morris, L., Level zero G-types. Compositio Math. 118(1999), 135–157. http://dx.doi.Org/10.1023/A:1001019027614 Google Scholar
[MP96] Moy, A. and Prasad, G., Jacquet functors and unrefined minimal K-types. Comment Math. Helv. 71(1996), 98–121. http://dx.doi.org/10.1007/BF02566411 Google Scholar
[MVW87] Moeglin, C., Vignéras, M.-F., and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique. Lecture Notes in Mathematics, 1291, Springer-Verlag, Berlin, 1987. http://dx.doi.Org/10.1OO7/BFbOO82712 Google Scholar
[MW03] Moeglin, C. and Waldspurger, J.-L, Paquets stables de repr괥ntations tempérées et deréduction unipotente pour SO(2n + 1). Invent. Math. 152(2003), 461–623. http://dx.doi.org/10.1007/s00222-002-0274-3 Google Scholar
[PanOl] Pan, S.-Y., Splittings of metaplectic covers of some reductive dual pairs. Pacific J. Math. 199(2001), 163–226. http://dx.doi.org/10.2140/pjm.2001.199.163 Google Scholar
[PanO2] Pan, S.-Y.,Local theta correspondence of representations of depth zero and theta dichotomy. J. Math. Soc. Japan 54(2002), 793–845. http://dx.doi.org/10.2969/jmsj71191591993 Google Scholar
[Ral82] Rallis, S., Langlands' functoriality and the Weil representation. Amer. J. Math. 104(1982), 469–515. http://dx.doi.org/10.2307/2374151 Google Scholar
[Sri79] Srinivasan, B., Weil representations of finite classical groups. Invent. Math. 51(1979), 143–153. http://dx.doi.Org/10.1007/BF01390225 Google Scholar
[Tat79] Tate, J., Number theoretic background. In: Automorphic forms, representations and L-functions II, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence, RI, 1979, pp. 3–26.Google Scholar
[Tit79] Tits, J., Reductive groups over local fields. In: Automorphic forms, representations and L-functions I, Proc. Sympos. Pure Math., 33, American Mathematical Society, Providence,RI, 1979, pp. 29–69.Google Scholar
[Wal90] Waldspurger, J.-L., Démonstration d' conjecture de dualité de Howe dans le case péadiques, p 2. In: Festschrift in honor of I. PiatetskiéShapiro on the occasion of his sixtieth birthday, Part I, Israel Math. Conf. Proc, 2, Weizmann, Jerusalem, 1990,nn. 267–324.Google Scholar