Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T07:46:23.257Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting Isomorphisms of Modules

Published online by Cambridge University Press:  20 November 2018

Irving Reiner
Irving Reiner*
Affiliation:
University of Illinois, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this note, let R be a discrete valuation ring with prime element π, residue class field 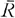, and quotient field K. Let Λ be an R-order in a finite dimensional K-algebra A. A Λ-lattice is an R-free finitely generated left Λ-module. For k > 0, we set

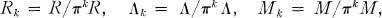
where M is any Λ-lattice. Obviously, for Λ-lattices M and N,

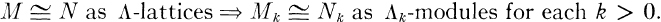
Maranda [1] and D. G. Higman [3] considered the reverse implication, and Proved

THEOREM. Let Λ be an R-order in a separable K-algebra A. Then there exists a positive integer k (which depends on Λ) with the following property: for each pair of Λ-lattices M and N,

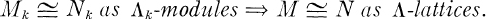
Indeed,m it suffices to choose k so that

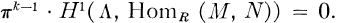
Maranda proved this result for the special case where Λ is the integral group ring RG of a finite group G.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 4 , 01 August 1979 , pp. 808 - 811
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Maranda, J. M., On p-adic integral representations of finite groups, Can. J. Math. 5 (1953), 344–355.Google Scholar
2. Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras (Wiley and Sons, New York, 1962).Google Scholar
3. Higman, D. G., On representations of orders over Dedekind domains, Can. J. Math. 12 (1960), 107–125.Google Scholar