Article contents
Limit Point Criteria for Differential Equations, II
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We consider here singular differential operators, and for convenience the finite singularity is taken to be zero. One operator discussed is the operator L defined by
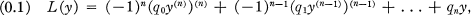
where q0 > 0 and the coefficients qt are real, locally Lebesgue integrable functions defined on an interval (a, b). For a given positive, continuous weight function h, conditions are given on the functions qi for which the number of linearly independent solutions y of L(y) = λhy (Re λ = 0) satisfying.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1974
References
1.
Dunford, N. and Schwartz, J., Linear operators. Part II (Interscience, New York, 1963).Google Scholar
2.
Hinton, D., Limit point criteria for differential equations, Can. J. Math.
24 (1972), 293–305.Google Scholar
4.
Walker, P. W., Asymptotic s for a class of weighted eigenvalue problems, Pacific J. Math.
40 (1972), 501–510.Google Scholar
- 10
- Cited by


